Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)

a.\(DK:\frac{2}{3}\le x< 4\)
b.\(DK:x>\frac{1}{2},x\ne\frac{5}{2}\)
c.\(DK:x\le-3\)
Bạn MaiLink ơi, bạn có thể ghi rõ ra các bước làm được không? mình không hiểu lắm. cảm ơn bạn

\(2,\\ a,\sqrt{4x-4}+\sqrt{9x-9}-\sqrt{25x-25}=7\left(x\ge1\right)\\ \Leftrightarrow2\sqrt{x-1}+3\sqrt{x-1}-5\sqrt{x-1}=7\\ \Leftrightarrow0\sqrt{x-1}=7\Leftrightarrow x\in\varnothing\\ b,\sqrt{2x^2-3}=4\left(x\le-\dfrac{\sqrt{6}}{2};\dfrac{\sqrt{6}}{2}\le x\right)\\ \Leftrightarrow2x^2-3=16\\ \Leftrightarrow x^2=\dfrac{19}{2}\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{19}{2}}\left(tm\right)\\x=-\sqrt{\dfrac{19}{2}}\left(tm\right)\end{matrix}\right.\)
\(1,\\ A=\sqrt{5+4x}+\sqrt{7-3x}\\ ĐKXĐ:\left\{{}\begin{matrix}5+4x\ge0\\7-3x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{5}{4}\\x\le\dfrac{7}{3}\end{matrix}\right.\)

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề hơn.

a) \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\) (ĐK: \(x\ne1,x\ge0\))
\(A=\left[\dfrac{x+2}{\left(\sqrt{x}\right)^3-1^3}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right]\cdot\dfrac{2}{\sqrt{x}-1}\)
\(A=\left[\dfrac{\left(x+2\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right]\cdot\dfrac{2}{\sqrt{x}-1}\)
\(A=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(A=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(A=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(A=\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(A=\dfrac{2}{x+\sqrt{x}+1}\)
b) Ta có:
\(A=\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}}=\dfrac{2}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\)
Mà: \(2>0\Rightarrow\dfrac{2}{\left(x+\dfrac{1}{2}\right)+\dfrac{3}{4}}\le\dfrac{2}{\dfrac{3}{4}}=\dfrac{8}{3}\)
Dấu "=" xảy ra:
\(\dfrac{2}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}=\dfrac{8}{3}\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=2:\dfrac{8}{3}\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\dfrac{3}{4}\Leftrightarrow x+\dfrac{1}{2}=0\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy: \(A_{max}=\dfrac{8}{3}\) khi \(x=-\dfrac{1}{2}\)
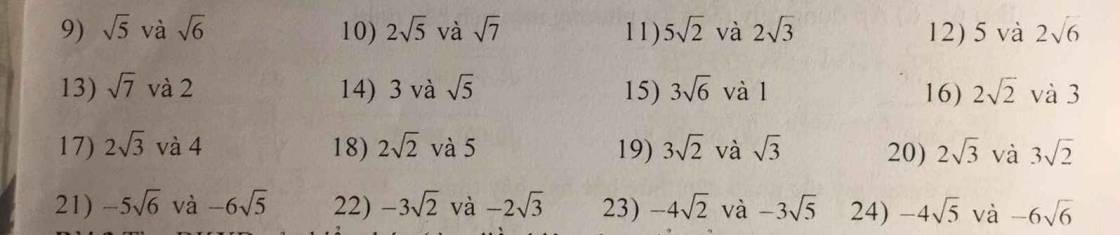
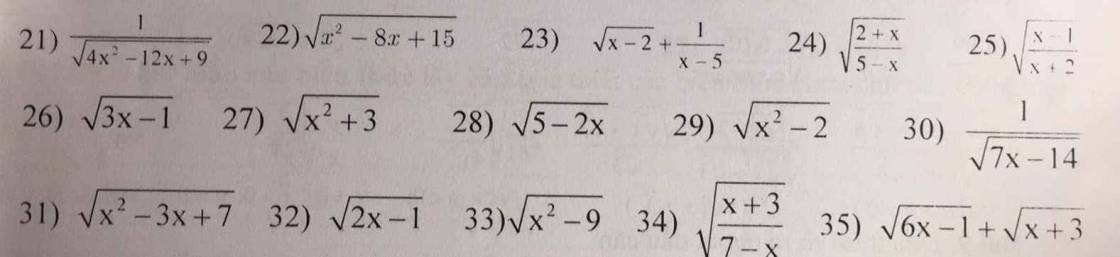

 (Với x > 0; x 1; x4)
(Với x > 0; x 1; x4)
\(\dfrac{1}{x}\)+ 2\(\sqrt{x-8}\)
ĐK: \(x\) ≠ 0; \(x\) - 8 ≥ 0; ⇒ \(x\) ≥ 8 vậy \(x\) ≥ 8