K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
1
26 tháng 11 2021
\(ĐK:x\ge0\\ PT\Leftrightarrow\left(x-\dfrac{3}{4}\right)\left(x^2+\dfrac{3}{4}x+\dfrac{9}{16}\right)\left(\sqrt{x}-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\left(n\right)\\\sqrt{x}=3\left(n\right)\\x^2+2\cdot\dfrac{3}{8}x+\dfrac{9}{64}+\dfrac{27}{64}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=9\\\left(x+\dfrac{3}{8}\right)^2+\dfrac{27}{64}=0\left(\text{vô nghiệm}\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=9\end{matrix}\right.\)
NT
3
CN
3
6 tháng 8 2015
<=> \(\frac{1.2.3....31}{4.6.8....64}=2^n\Rightarrow\frac{1.2.3....30.31}{2\left(2.3.4.5...31\right).32}=2^n\Leftrightarrow\frac{1}{2.32}=2^n\Leftrightarrow\frac{1}{2^6}=2^n\)
=> 2^6.2^n = 1
=> 2^ (n + 6 ) = 2^0
=> n+ 6 = 0
=> n = - 6
DD
6 tháng 8 2015
\(\frac{1}{4}.\frac{2}{6}.\frac{3}{8}....\frac{31}{64}=\frac{1.2.3....31}{4.6.8....64}=\frac{1.2.3....31}{2.3.2.4....2.32}=\frac{1.2.3....31}{2^{30}.\left(3.4....32\right)}=\frac{2}{2^{30}.32}=\frac{1}{2^{34}}=2^{-34}=2^n=>n=-34\)
HN
1
16 tháng 4 2023
\(\dfrac{M}{N}=\dfrac{x^4-x^3+6x^2-x+a}{x^2-x+5}\)
\(=\dfrac{x^4-x^3+5x^2+x^2-x+5+a-5}{x^2-x+5}\)
\(=x^2+1+\dfrac{a-5}{x^2-x+5}\)
Để M chiahết cho N thì a-5=0
=>a=5
Để M chia N dư 3 thì a-5=3
=>a=8
b) x2 – 4x +3
18 tháng 6 2023
a: P(x)=6x^3-4x^2+4x-2
Q(x)=-5x^3-10x^2+6x+11
M(x)=x^3-14x^2+10x+9
b: \(C\left(x\right)=7x^4-4x^3-6x+9+3x^4-7x^3-5x^2-9x+12\)
=10x^4-11x^3-5x^2-15x+21
KH
8 tháng 7 2021
\(a.\left(x+5\right)^3=-64\Leftrightarrow x+5=-4\Leftrightarrow x=-9\\ b.\left(2x-3\right)^2=9\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
( Nhớ kết luận! )
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
a.
\(\left(x+5\right)^3=\left(-4\right)^3\)
\(\Leftrightarrow x+5=-4\)
\(\Leftrightarrow x=-9\)
b.
\(\left(2x-3\right)^2=3^2\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
CM
23 tháng 6 2017
Chọn C
Ta có: P(x) + Q(x) = x3+ x2+ 2x-1
⇒ Q(x) = (x3 + x2 + 2x-1) - P(x)
= 2x3 + 4x2 - 8x - 3.
19 tháng 9 2023
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
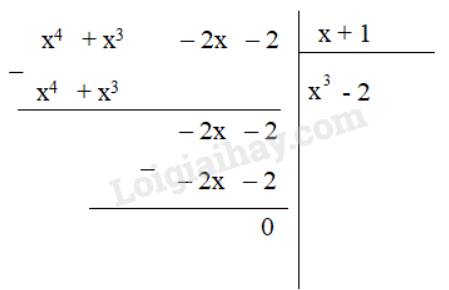
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
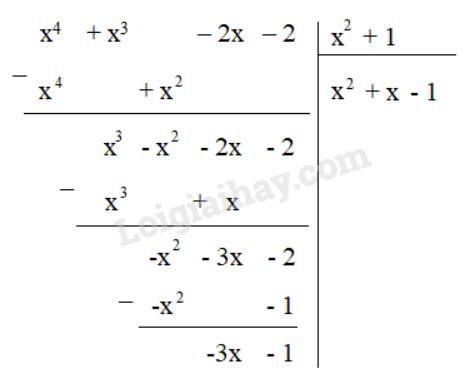
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn
a) x3 = 64
Ta có: 64 = 43. Do đó x3 = 43 nên x = 4.
Vậy x = 4 là giá trị cần tìm.
x³ = 64
x³ = 4³
x = 4