Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Có y ' = − 3 x 2 + 4 m x − m 2 .
Hàm số đạt cực tiểu tại x = 1 ⇒ y ' 1 = 0 ⇒ m = 1 m = 3
Với m = 1 thì y' đổi dấu + sang – qua x=0 nên x=0 là cực đại (Loại)
Với m = 3 thì y' đổi dấu - sang + qua x=0 nên x=0 là cực tiểu (tm)

Đáp án C
Có y ' = − 6 x 2 + 6 m x ; y ' = 0 ⇔ x = 0 x = m .
Hàm số đạt cực tiểu tại x = 0 ⇔ m < 0 .

Đáp án A
Ta có y ' = 3 m x 2 + 2 x + m 2 − 6 ⇒ y ' ' = 6 m x + 2
Hàm số đạt cực tiểu tại x = 1 ⇒ y ' 1 = 3 m + 2 + m 2 − 6 = 0 ⇔ m = 1 m = − 4
Với m = − 4 ⇒ y ' ' 1 = 6 m + 2 = − 22 < 0 nên hàm số đạt cực đại tại x = 1
Với m = 1 ⇒ y ' ' 1 = 6 m + 2 = 8 > 0 nên hàm số đạt cực tiểu tại x = 1

Đáp án D
Phương pháp:
Điểm x = x 0 là điểm cựa tiểu của hàm số bậc ba y = f x nếu f ' x 0 = 0 f ' ' x 0 > 0
Cách giải:
TXĐ: D = R
Ta có: y ' = 3 x 2 − 4 m x + m 2 → y ' ' = 6 x − 4 m
Để x=1 là điểm cực tiểu của hàm số bậc ba với hệ số x 3 dương thì:
y ' 1 = 0 y ' ' 1 > 0 ⇔ m 2 − 4 m + 3 = 0 6 − 4 m > 0 ⇔ m = 1 ; m = 3 m < 3 2 ⇔ m = 1
Chú ý khi giải:
Nhiều HS sẽ nhầm lẫn điều kiện để điểm x 0 là điểm cực tiểu là f ' ' x 0 > 0 dẫn đến chọn đáp án m=3 là sai

Đáp án B.
Phương pháp:
Hàm số y = f x đạt cực tiểu tại
M x 0 ; y 0 ⇔ f x 0 = y 0 f ' x 0 = 0 f ' ' x 0 > 0
Cách giải:
y = 1 3 s 3 − 1 2 2 m + 3 x 2 + m 2 + 3 m − 4 x = f x ⇒ y ' = f ' x = x 3 − 2 m + 3 x + m 2 + 3 m − 4 ,
y " = f " x = 2 x − 3 m − 3
Hàm số
y = 1 3 x 3 − 1 2 2 m + 3 x 3 + m 2 + 3 m − 4 x
đạt cực tiểu tại
x = 1 ⇔ f ' 1 = 0 f " 1 > 0
⇔ 1 − 3 m − 3 + m 2 + 3 m − 4 = 0 2 − 2 m − 3 > 0 ⇔ m 2 + m − 6 = 0 m < − 1 2 ⇔ m = − 3 m = 2 m < − 1 2 ⇔ m = − 3.

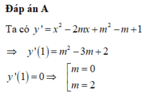
+ Với m=0 khi đó phương trình y’ = 0 sẽ có nghiệm kép nên loại.
+ Với m=2 thì khi đó phương trình y’=0 có hai nghiệm.
Chọn phương án A.

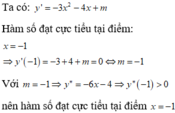
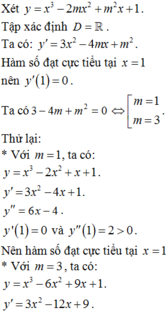

Đáp án C.
Ta có y ' = 4 x 3 − 4 m + 1 x = 4 x x 2 − m − 1 .
Hàm trùng phương với hệ số a > 0 có 2 dạng:
+) Có 2 cực tiểu và 1 cực đại tại x = 0 ⇒ y ' = 0 có 3 nghiệm phân biệt.
+) có 1 cực tiểu tại x = 0 ⇒ y ' = 0 có 1 nghiệm x = 0.
Hàm số đã cho đạt cực tiểu tại x = 0 ⇔ m + 1 ≤ 0 ⇔ m ≤ − 1.