Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=\dfrac{mx+6}{2x+m+1}\Rightarrow y'=\dfrac{m\left(m+1\right)-12}{\left(2x+m+1\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}m\left(m+1\right)-12< 0\\\left[{}\begin{matrix}-\dfrac{m+1}{2}>1\\-\dfrac{m+1}{2}< -1\end{matrix}\right.\\\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-4< m< 3\\\left[{}\begin{matrix}m< -3\\m>1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-4< m< -3\\1< m< 3\end{matrix}\right.\)

Chọn A
Phương pháp:
Tính y'.
Điều kiện để hàm số đã cho nghịch biến trên - ∞ ; 1 là
Cách giải:
Tập xác định ![]()
Ta có 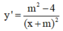
Để hàm số nghịch biến trên khoảng
-
∞
;
1
![]()


Chọn B.
Tập xác định ![]()
Có 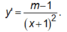
Hàm số nghịch bến trên mỗi khoảng của tập xác định
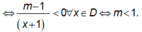

Chọn D.
![]()
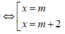
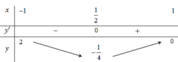
Do đó ta có bảng biến thiên sau:
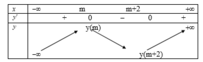
Để hàm số nghịch biến trên khoảng (-1;1) thì
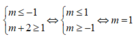
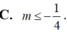
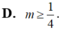

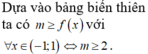

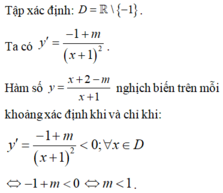


Ta có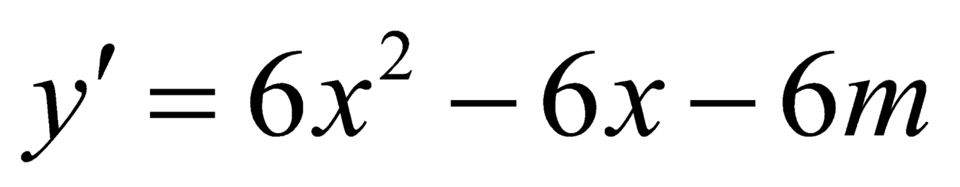 .
.
Hàm số nghịch biến trên khoảng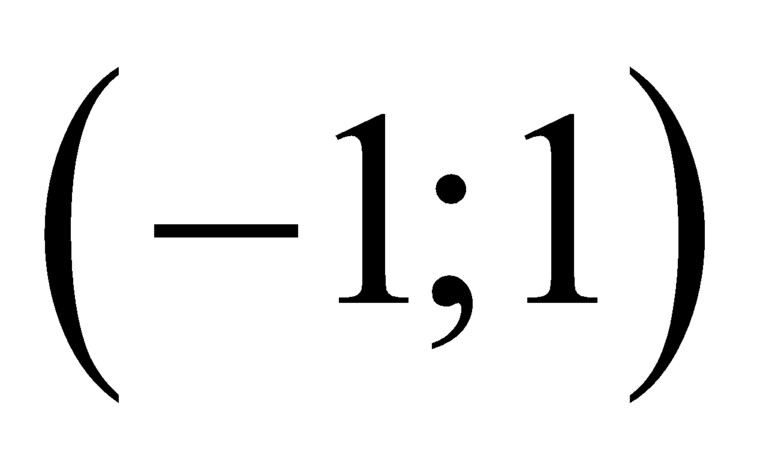 khi và chỉ khi
khi và chỉ khi 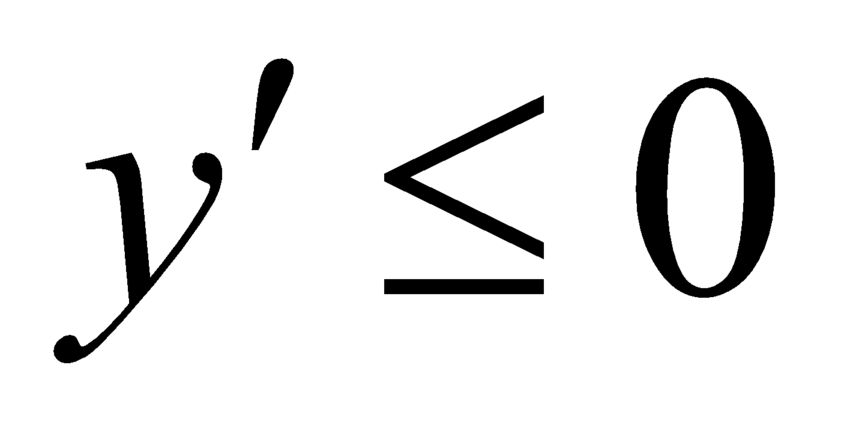 với
với 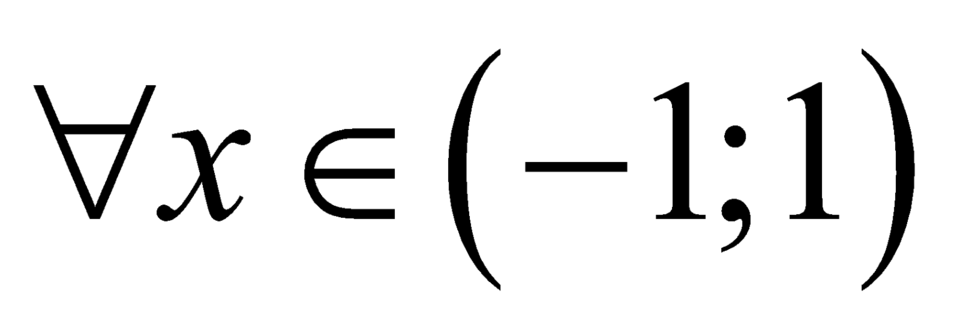 hay
hay 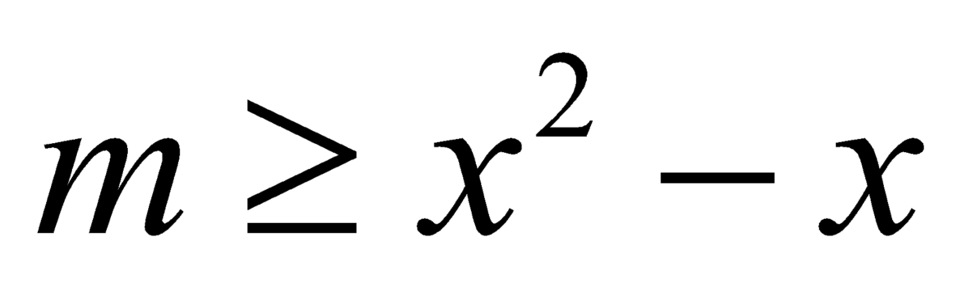 với
với 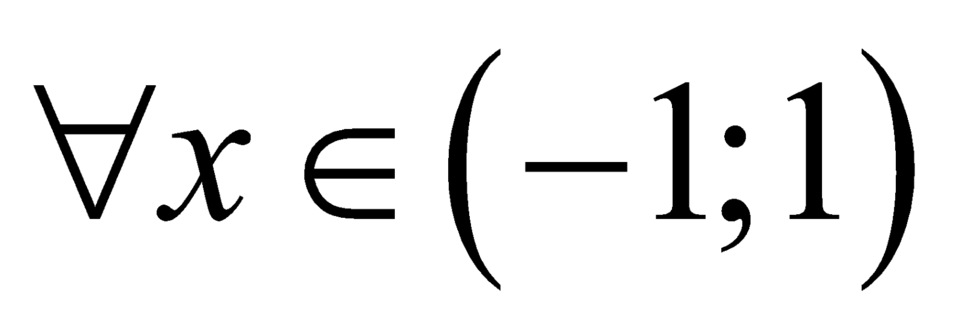 .
.
Xét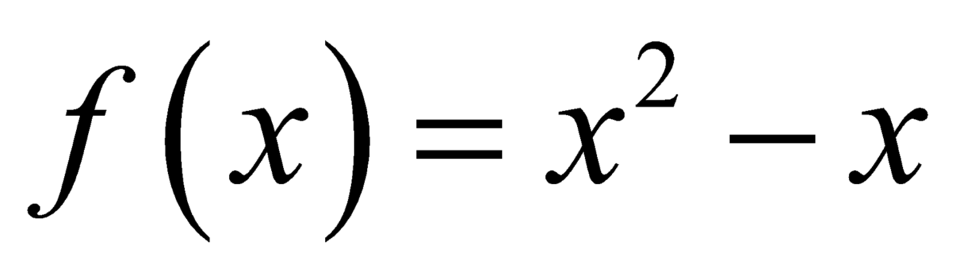 trên khoảng
trên khoảng 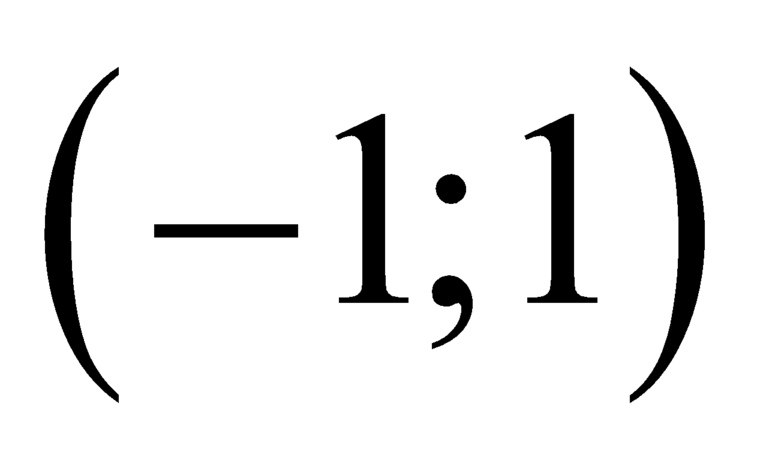 ta có
ta có
Bảng biến thiên
Dựa vào bảng biến thiên ta có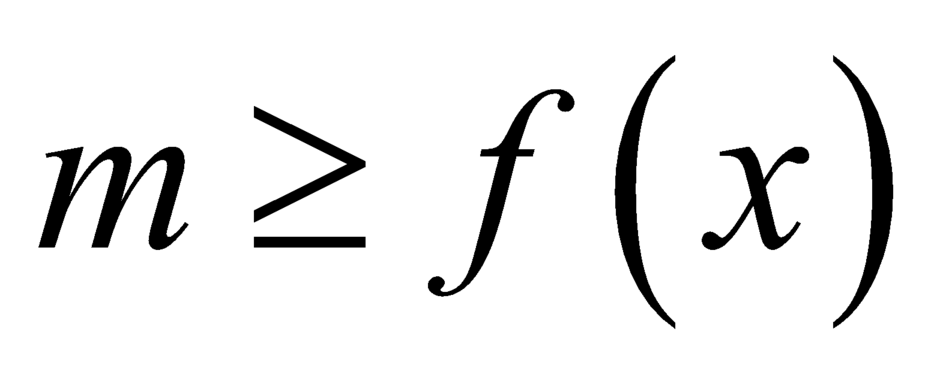 với
với 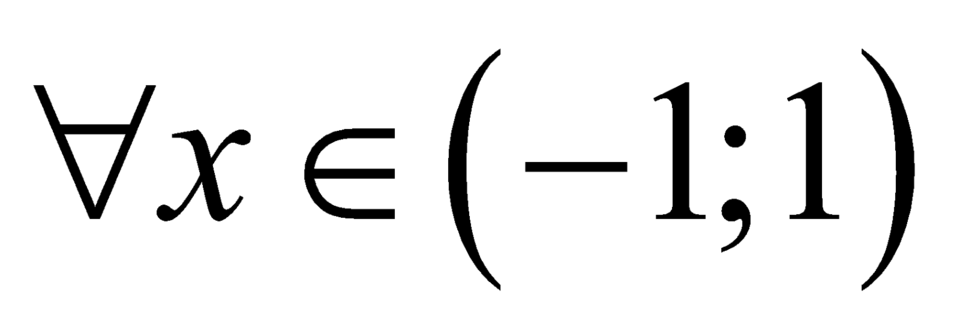
Đáp án A