Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
giả sử : \(\frac{mx+m}{\left(m+1\right)x-m+2}>0\)\(,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{m.0+m}{\left(m+1\right).0-m+2}>0\) \(\Rightarrow\frac{m}{2-m}>0\)
\(\Rightarrow0\)\(<\)\(m<\)\(2\)
ngược lại \(0<\)\(m<2\) thì:
\(mx+m>0,\text{∀}x\in\left[0;2\right]\)
\(\left(m+1\right)x\ge0>m-2,\)\(\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\left(m+1\right)x-m+2>0,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{mx+m}{\left(m+1\right)x-m+2}>0,\text{∀}x\in\left[0;2\right]\)
vậy: \(0\)\(<\)\(m<\)\(2\) là kết quả cần tìm
Đáp án C
6 x − 3 − m 2 x − m = 0 ⇔ m = 6 x + 3.2 x 2 x + 1
Xét hàm số f x = 6 x + 3.2 x 2 x + 1 trên khoảng 0 ; 1
f ' x = 6 x .2 x ln 6 − ln 2 + 6 x ln 6 + 3.2 x ln 2 2 x + 1 2 > 0 do đó hàm số y = f x đồng biến trên khoảng 0 ; 1 .
Phương trình f x = m có nghiệm trong khoảng 0 ; 1 ⇔ f 0 < m < f 1 ⇔ 2 < m < 4 .
Đáp án C
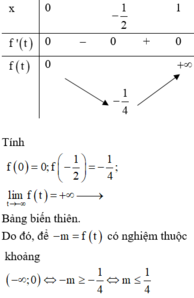
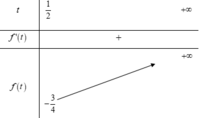
log 2 2 2 x − 2 m + 1 log 2 x − 2 < 0 ⇔ 1 + log 2 x 2 − 2 m + 1 log 2 x − 2 < 0
Đặt t = log 2 x ta được 1 + t 2 − 2 m + 1 t − 2 < 0 ⇔ t 2 − 2 m t − 1 < 0 ⇔ t ∈ m − m 2 + 1 ; m + m 2 + 1
x ∈ 2 ; + ∞ ⇔ t ∈ 1 2 ; + ∞
⇒ m + m 2 + 1 > 1 2 ⇔ m > − 3 4
Bất phương trình đã cho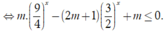 
Đặt 
Bất phương trình trở thành 
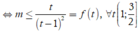
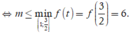
Chọn D.
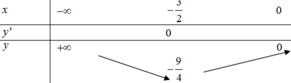
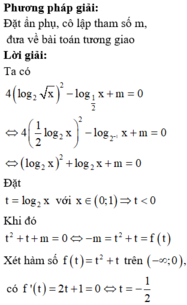
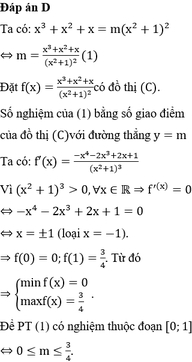
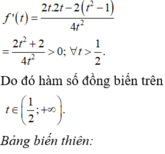
với \(m=0\) : PT \(\left(1\right)\Leftrightarrow\) \(-2x+1=0\) \(\Leftrightarrow x=\frac{1}{2}\in\left(0;1\right)\)
với \(m\ne0\) : PT \(\left(1\right)\) có đúng 1 nghiệm \(\in\left(0;1\right)\)
\(\Leftrightarrow f\left(0\right).f\left(1\right)<0\)
( để ý: \(\Delta'=\left(m+1\right)^2-m=\)\(m^2+m+1>0,\text{∀}x\in R\))
\(\Leftrightarrow m-2\left(m+1\right)+1<0\) \(\Leftrightarrow m>-1\)
vậy \(m>-2\) là kết quả cần tìm
với m=0m=0 : PT (1)⇔(1)⇔ −2x+1=0−2x+1=0 ⇔x=12∈(0;1)⇔x=12∈(0;1)
với m≠0m≠0 : PT (1)(1) có đúng 1 nghiệm ∈(0;1)∈(0;1)
⇔f(0).f(1)<0⇔f(0).f(1)<0
( để ý: Δ′=(m+1)2−m=Δ′=(m+1)2−m=m2+m+1>0,∀x∈Rm2+m+1>0,∀x∈R)
⇔m−2(m+1)+1<0⇔m−2(m+1)+1<0 ⇔m>−1⇔m>−1
vậy m>−2m>−2 là kết quả cần tìm