Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=10 vào (d1), ta được:
\(y=2\cdot10-1=20-1=19\)
=>A(10;19) thuộc (d1)
Thay x=-4 vào (d1), ta được:
\(y=2\left(-4\right)-1=-8-1=-9\)
=>B(-4;-7) không thuộc (d1)
Thay x=-11 vào (d1), ta được:
\(y=2\cdot\left(-11\right)-1=-22-1=-23\)
=>C(-11;-23) thuộc (d1)
b: 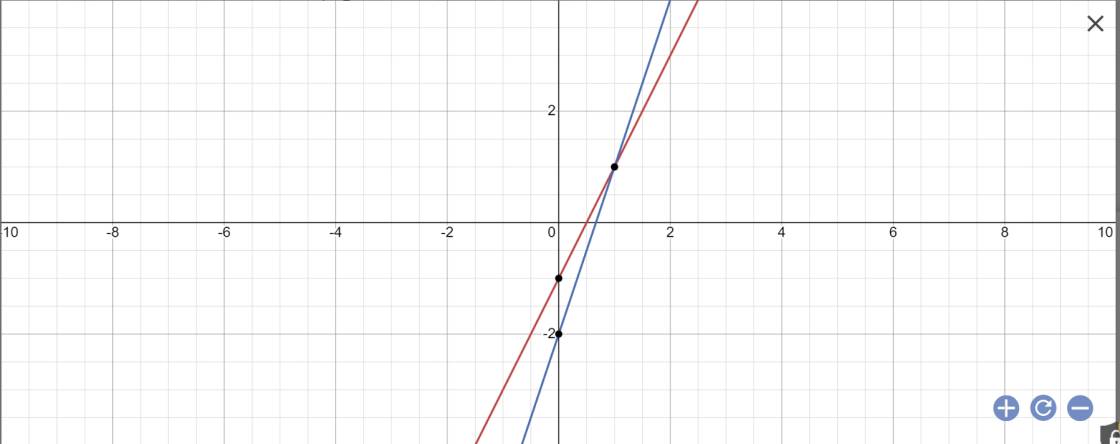
c: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-2=2x-1\\y=2x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2x=-1+2=1\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\cdot1-1=1\end{matrix}\right.\)
d: Để (d3) đồng quy với (d1),(d2) thì (d3) đi qua giao điểm của (d1) và (d2)
=>(d3) đi qua F(1;1)
Thay x=1 và y=1 vào (d3), ta được:
1(m-1)+3=1
=>m-1+3=1
=>m+2=1
=>m=-1

a: Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=5\\2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)
b:
1: Thay x=-1 và y=3 vào (d), ta được:
\(2\cdot\left(-1\right)-a+1=3\)
=>-a-1=3
=>-a=4
hay a=-4

Bài 2 :
\(\hept{\begin{cases}3x+2y=11\left(1\right)\\x+2y=5\left(2\right)\end{cases}}\)
Lấy phương trình (1) - phương trình (2) ta được :
\(2x=6\Leftrightarrow x=3\)
Thay x = 3 vào phương trình (2) ta được :
\(3+2y=5\Leftrightarrow2y=2\Leftrightarrow y=1\)
Vậy \(\left(x;y\right)=\left(3;1\right)\)

Lời giải:
a)
\(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3=4a+b\\ -7=-6a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1\\ b=-1\end{matrix}\right.\)
b)
\(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -1=3a+b\\ -2=-3a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{1}{6}\\ b=\frac{-3}{2}\end{matrix}\right.\)
c)
\(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 1=2a+b\\ 2=a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=-1\\ b=3\end{matrix}\right.\)
d)
\(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3=a+b\\ 2=3a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{-1}{2}\\ b=\frac{7}{2}\end{matrix}\right.\)

Thay tọa độ điểm A vào phương trình đường thẳng ta được 2a + b = 1
Thay tọa độ điểm B vào phương trình đường thẳng ta được −2a + b = 3
Từ đó ta có hệ phương trình
2 a + b = 1 − 2 a + b = 3 ⇔ b = 1 − 2 a − 2 a + 1 − 2 a = 3 ⇔ a = − 1 2 b = 1 − 2. − 1 2 ⇔ a = − 1 2 b = 2
Vậy a = − 1 2 ; b = 2
Đáp án: A
Thay tọa độ điểm M vào phương trình đường thẳng ta được 3a + b = −5
Thay tọa độ điểm N vào phương trình đường thẳng ta được a + b = 2
Từ đó ta có hệ phương trình
a + b = 2 3 a + b = − 5 ⇔ b = 2 − a 3 a + 2 − a = − 5 ⇔ b = 2 − a 2 a = − 7 ⇔ a = − 7 2 b = 11 2
Vậy a = − 7 2 ; b = 11 2
Đáp án: D