Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Gọi hai số tự nhiên cần tìm là a và b
Ta có : \(a=6.k_1;b=6.k_2\)
Trong đó : \(ƯCLN\left(k_1,k_2\right)=1\)
Mà : \(a+b=84\Rightarrow6.k_1+6.k_2=84\)
\(\Rightarrow6\left(k_1+k_2\right)=84\Rightarrow k_1+k_2=84\div6=14\)
+) Nếu : \(k_1=1\Rightarrow k_2=13\Rightarrow\begin{cases}a=6\\b=78\end{cases}\)
+)Nếu : \(k_1=3\Rightarrow k_2=11\Rightarrow\begin{cases}a=18\\b=66\end{cases}\)
+)Nếu : \(k_1=5\Rightarrow k_2=9\Rightarrow\begin{cases}a=30\\b=54\end{cases}\)
Vậy ...
b, Tương tự câu a,
c, Gọi hai số tự nhiên cần tìm là a và b
Vì : \(ƯCLN\left(a,b\right)=10;BCNN\left(a,b\right)=900\)
\(\RightarrowƯCLN\left(a,b\right).BCNN\left(a,b\right)=a.b=900.10=9000\)
Phần còn lại giống câu a và câu b tự làm

a) n=7k+1 ( \(k\in N\))
b) 18 va 66 hoac 6 va 78 hoac 30 va 54
c) 15 va 20 hoac 5 va 60
d) 10 va 900 hoac 20 va 450 hoac 180 va 50 hoac 100 va 90

Gọi các số phải tìm là a và b, giả sử a < b. Ta có ( a, b ) = 10 nên a = 10a', b = 10b', ( a', b' ) = 1, a' < b'. Do đó ab = 100a'b' ( 1 ). Mặt khác ab [ a, b ] . ( a, b ) = 900.10 = 9000 ( 2 )
Từ ( 1 ) và ( 2 ) suy ra a'b' = 90. Ta có các trường hợp
| a' | 1 | 2 | 5 | 9 |
| b' | 90 | 45 | 18 | 10 |
Do đó
| a | 10 | 20 | 50 | 90 |
| b | 900 | 450 | 180 | 100 |
3) Tìm ƯCLN của hai số bằng thuật toán Ơ - clit.

a, Gọi hai số phải tìm là a,b. Ta có (a;b) = 6 => a = 6a’, b = 6b’ với (a’,b’) = 1(a,b,a’,b’ ∈ N)
Do đó: a+b = 84 => 6.(a’+b’) = 84 => a’+b’ = 14
Chọn cặp số a’,b’ là hai số nguyên tố cùng nhau có tổng bằng 14 ta được:
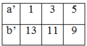
Do đó:
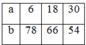
b, Gọi hai số phải tìm là a.b. Ta có (a;b) = 5 => a = 5a’, b = 5b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N)
Do ab = 300 => 25a’b’ = 300 => a’b’ = 12 = 4.3
Chọn cặp số a’,b’ nguyên tố cùng nhau có tích bằng 12 ta được:
a’ = 1, b’ = 12 => a = 5, b = 60
a’ = 3, b’ = 4 => a = 15, b = 20
c, Gọi hai số phải tìm là a,b. Ta có (a;b) = 10 => a = 10a’; b = 10b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N, a’<b’). Do đó: ab = 100a’b’ (1)
Mặt khác: ab = [a,b].(a,b) = 900.10 = 9000 (2)
a’ = 1, b’ = 90 => a = 10, b = 900
a’ = 2, b’ = 45 => a = 20, b = 450
a’ = 5, b’ = 18 => a = 50, b = 180
a’ = 9, b’ = 10 => a = 90, b = 100

Gọi các số phải tìm là a và b, giả sử a < b. Ta có ( a, b ) = 10 nên a = 10a', b = 10b', ( a', b' ) = 1, a' < b'. Do đó ab = 100a'b' ( 1 ). Mặt khác ab [ a, b ] . ( a, b ) = 900.10 = 9000 ( 2 )
Từ ( 1 ) và ( 2 ) suy ra a'b' = 90. Ta có các trường hợp
| a' | 1 | 2 | 5 | 9 |
| b' | 90 | 45 | 18 | 10 |
Do đó
| a | 10 | 20 | 50 | 90 |
| b | 900 | 450 | 180 | 100 |
Lời giải:
Gọi 2 số tự nhiên cần tìm là $a$ và $b$. Coi $a$ là số lớn hơn. Gọi $d$ là ƯCLN của $a,b$. Khi đó, đặt:
$a=dx, b=dy$ thì $x,y$ là 2 số nguyên tố cùng nhau và $x>y$
BCNN $(a,b)=dxy$. Ta có:
$ab=dx.dy=d^2xy=2700$
$dxy=900(1)$
$\Rightarrow d=(d^2xy):(dxy)=2700:900=3$
Thay vào $(1)$ suy ra $xy=300=2^2.3.5^2$
Vì $x,y$ nguyên tố cùng nhau và $x>y$ nên: $(x,y)=(300,1); (25,12), (100,3); (75, 4)$
$\Rightarrow (a,b)=(900,3); (75, 36); (300,9); (225, 12)$
a) Gọi hai số tự nhiên cần tìm là a và b.
Ta có: ab = 2700 và [a,b] = 900
Ta có tính chất: (a,b).[a,b] = ab
=> (a,b). 900 = 2700
=> (a,b) = 2700 : 900
=> (a,b) = 3
=> a = 3m và b = 3n [(m,n) = 1]
=> ab = 3m.3n = 9mn = 2700
=> mn = 2700 : 9
=> mn = 300
Mà (m,n) = 1 nên m = 1 và n = 300 hoặc ngược lại.
=> a = 3, b = 900 hoặc a = 900 , b = 3
Nhớ vote nha bn