NT
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Q
1
8 tháng 9 2015
Vậy Với a = c = 0; 1 ... đến 9 ; và b = d = 0 thỏa mãn yêu cầu
7 tháng 9 2015
b)
0,0ab + a,bab = 4,896
Nhân các số ở cả 2 vế với 1000 ta được:
ab + abab = 4896
ab x 1 + ab x 100 + ab x 1 = 4896
ab x (1 + 100 + 1) = 4896
ab x 102 = 4896
ab = 4896 : 102 = 48
Vậy ab = 48
c) Nhân cả 2 vế với 100 ta được:
41,ab x 100 = (a,b x 10) x (2,6 x 10)
41ab = ab x 26
4100 + ab = 26 x ab
4100 = 25 x ab
ab = 4100 : 25 = 164 Vô lí vì ab là số có 2 chữ số
vậy không có số a; b thỏa mãn
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
24 tháng 6 2023
a, \(\overline{ab,b}\) - \(\overline{c,c}\) = \(\overline{0,a}\)
(\(\overline{ab,b}\) - \(\overline{c,c}\)) \(\times\)10 = \(\overline{0,a}\)
\(\overline{abb}\) - \(cc\) = \(a\)
\(a\times\)100 + \(b\)\(\times\)11 - \(c\times\)11 = \(a\)
\(a\times\)100 + \(b\times\)11 - \(c\times\)11 - \(a\) = 0
\(a\times\)99 + \(b\) \(\times\)11 - \(c\times\) 11 = 0
11\(\times\)(\(a\times\)9 + \(b\) - \(c\)) = 0
\(a\times\) 9 + \(b\) - \(c\) = 0
\(a\times\) 9 = \(c-b\) ⇒ \(c-b\)⋮9 ⇒ \(c\) = \(b\) ; \(c\) - \(b\) = 9;
th: \(c\) = \(b\) ⇒ \(a\times\)9 = 0 ⇒ \(a\) = 0 (loại)
th: \(c-b=9\) ⇒ \(c=9+b\) ⇒ \(b\) = 0; \(c\) = 9
\(a\times\) 9 = 9 - 0 = 9 ⇒ \(a\) = 1
Vậy thay \(a=1;b=0;c=9\) vào biểu thức: \(\overline{ab,b}-\overline{c,c}=\overline{o,a}\) ta được:
10,0 -9,9 = 0,1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
24 tháng 6 2023
b, \(\overline{b,a}\) - \(\overline{a,b}\) = 2,7
(\(\overline{b,a}\) - \(\overline{a,b}\))\(\times\)10 = 2,7 \(\times\) 10
\(\overline{ba}\) - \(\overline{ab}\) = 27
\(b\times10+a-a\times10-b\) = 27
(\(b\times10\) - \(b\)) - (\(a\) \(\times\) 10 - \(a\)) = 27
(\(b\times10-b\times1\)) - (\(a\times\)10 - \(a\)\(\times\)1) = 27
\(b\)\(\times\)(10 -1) - \(a\) \(\times\)( 10 - 1) =27
\(b\times\) 9 - \(a\times9\) = 27
9\(\times\) (\(b-a\)) = 27
\(b-a\) = 27 : 9
\(b-a\) = 3 ⇒ \(b\) = 3 + \(a\) ≤ 9 ⇒ \(a\) ≤ 9 - 3 = 6
Lập bảng ta có:
| \(a\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(b\) = \(a+3\) | 3 | 4 | 5 | 6 | 7 | 8 |
9 |
Thay các giá trị của \(a;b\) lần lượt vào biểu thức \(\overline{b,a}-\overline{a,b}\) = 2,7 ta có:
3,0 - 0,3 = 2,7
4,1 - 1,4 = 2,7
5,2 - 2,5 = 2.7
6,3 - 3,6 = 2,7
8,5 - 5,8 = 2,7
9,6 - 6,9 = 2,7
DH
2
24 tháng 10 2014
chiu thui , minh lam bai on thi nhiu rui bay gio suy nghi cai nay nhuc dau lam
21 tháng 2 2021
a,bcaa = c,baba + b,dbc
Nhân cả 2 vế với 10 000 ta được :
abcaa = cbaba + bdbc0
a00aa + b000 + c00 = c0000 + b0b0 + a0a + b0b00 + d000 + c0
(a x 10 000 + a x 10 + a) + (b x 1000) + (c x 100) = (c x 10 000 + c x 10) + (b x 10 000 + b x 1000 + b x 100 + b x 10) + (d x 1000) + (a x 100 + a)
a x 9 910 = b x 10 110 + c x 9 910 + d x 1000
a x 991 = b x 1011 + c x 991 + d x 100 (*)
a x 991 = b x 991 + c x 991 + b x 20 + d x 100
a x 991 = (b +c) x 911 + b x 20 + d x 100
=> (b + c) x 991 < a x 991 => b + c < hoặc bằng a
Từ (*) ta có: Vế trái có tận cùng là chữ số a; Vế phải có tận cùng là chữ số tận cùng của tổng b + c. Mà b + c < hoặc bằng a
=> a = b + c
=> b x 20 + d x 100 = 0 => b = d = 0 => a = c
Lại có : a là chữ số nên a = c = 0; 1; 2; ... đến 9; b = d = 0
Vậy Với a = c = 0; 1 ... đến 9 ; và b = d = 0 thỏa mãn yêu cầu
10 tháng 3 2019
A, abc=789
B, Không có giá trị abc nào thỏa mãn đề bài do 3abc-abc=3000
C, không có giá trị nào của abc thỏa mãn đề bài do 12ab-26=ab nên 12ab-ab=26 mà 12ab-ab=1200
PT
1
CM
11 tháng 6 2017
Ta có : abab = 101 x ab
101 x ab + ab = 1326
102 x ab = 1326
ab = 13
PT
1
PT
1
CM
14 tháng 9 2018
a) Ta viết lại thành phép nhân:
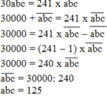
b) Ta có: abab = 101 x ab
101 x ab + ab = 1326
102 x ab = 1326
ab = 13
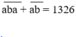
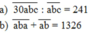
a,bcaa = c,baba + b,dbc
Nhân cả 2 vế với 10 000 ta được :
abcaa = cbaba + bdbc0
a00aa + b000 + c00 = c0000 + b0b0 + a0a + b0b00 + d000 + c0
(a x 10 000 + a x 10 + a) + (b x 1000) + (c x 100) = (c x 10 000 + c x 10) + (b x 10 000 + b x 1000 + b x 100 + b x 10) + (d x 1000) + (a x 100 + a)
a x 9 910 = b x 10 110 + c x 9 910 + d x 1000
a x 991 = b x 1011 + c x 991 + d x 100 (*)
a x 991 = b x 991 + c x 991 + b x 20 + d x 100
a x 991 = (b +c) x 911 + b x 20 + d x 100
=> (b + c) x 991 < a x 991 => b + c < hoặc bằng a
Từ (*) ta có: Vế trái có tận cùng là chữ số a; Vế phải có tận cùng là chữ số tận cùng của tổng b + c. Mà b + c < hoặc bằng a
=> a = b + c
=> b x 20 + d x 100 = 0 => b = d = 0 => a = c
Lại có : a là chữ số nên a = c = 0; 1; 2; ... đến 9; b = d = 0
Vậy Với a = c = 0; 1 ... đến 9 ; và b = d = 0 thỏa mãn yêu cầu
a = c là các chữ số từ 0 đến 9 và b = d = 0 thỏa mãn đề bài.