HL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HL
0
22 tháng 9 2015
1. \(\frac{x}{y}=\frac{7}{17}\)
3. Có 6 cặp
4. 0 có cặp nào hết
Câu 2 mình không biết nha. Thông cảm
7 tháng 12 2015
1)
\(xy-y=x\Leftrightarrow y=\frac{x}{x-1}=1+\frac{1}{x-1}\)
y thuộc Z => x -1 thuộc U(1) ={ -1;1}
+x =-1 => y =0
+x =1 => y =2
2) \(x.\left(1-\frac{1}{7}\right)<1\frac{6}{7}\Leftrightarrow x.\frac{6}{7}<\frac{13}{7}\Rightarrow x<\frac{13}{7}.\frac{7}{6}=\frac{13}{6}=2,1\left(6\right)\)
x thuộc Z+ => x thuộc {1;2}
TH
7 tháng 12 2015
Bài này bạn đăng rồi Nguyễn Nhật Minh trả lời đúng rồi mà :
http://olm.vn/hoi-dap/question/314450.html
NH
0
TH
2
28 tháng 1 2017
\(\frac{x}{6}-\frac{1}{y}=\frac{1}{2}\)
\(\Rightarrow\frac{x}{6}-\frac{1}{2}=\frac{1}{y}\)
\(\Rightarrow\frac{x}{6}-\frac{3}{6}=\frac{1}{y}\)
\(\Rightarrow\frac{x-3}{6}=\frac{1}{y}\)
\(\Rightarrow\left(x-3\right)y=6\)
Ta có bảng sau:
...
NL
3
7 tháng 1 2018
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{ab}\)
=> \(\frac{a+b}{ab}=\frac{1}{ab}\)=> a+b=1 => a,b là số nguyên sao cho a+b=1
7 tháng 1 2018
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{ab}\)
\(\frac{b}{ab}+\frac{a}{ab}=\frac{1}{ab}\)
\(\frac{b+a}{ab}=\frac{1}{ab}\)
\(\Rightarrow b+a=1\)
Vậy các giá trị nguyên của a,b phụ thuộc vào b + a = 1
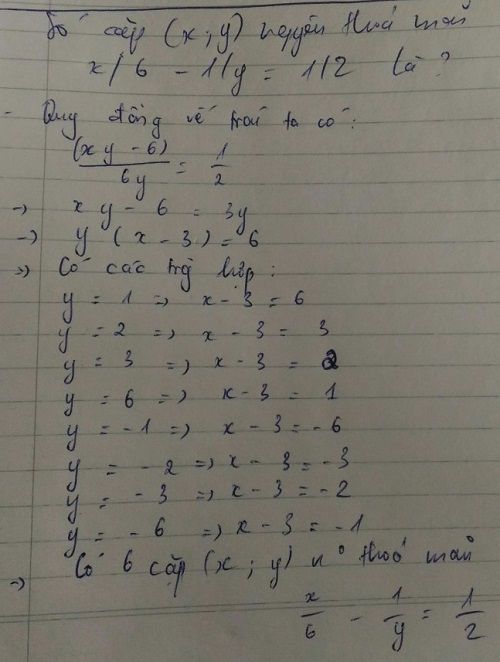
Ta có: \(\frac{1}{a}-\frac{1}{b}=\frac{1}{a-b}\)
=> \(\frac{b}{ab}-\frac{a}{ab}=\frac{1}{a-b}\)
=> \(\frac{b-a}{ab}=\frac{1}{a-b}\)
=> (b-a)(a-b)=ab.1
=> (b-a)(a-b)=ab (1)
Mà b-a và a-b trái dấu
Nên (b-a)(a-b)= -ab (2)
Từ (1), (2)=>không có cặp số nguyên x,y thỏa mãn