Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta cần tính góc \(\widehat A\) và hai cạnh \(b,c.\)
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {44^o}30' - {64^o} = {71^o}30'.\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{17,4}}{{\sin {{71}^o}30'}} = \frac{b}{{\sin {{44}^o}30'}} = \frac{c}{{\sin {{64}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}b = \sin {44^o}30'.\frac{{17,4}}{{\sin {{71}^o}30'}} \approx 12,86\\c = \sin {64^o}.\frac{{17,4}}{{\sin {{71}^o}30'}} \approx 16,5\end{array} \right.\end{array}\)
b) Ta cần tính số đo ba góc \(\widehat A,\widehat B,\widehat C\)
Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \cos A = \frac{{{6^2} + {8^2} - {{10}^2}}}{{2.6.8}} = 0;\cos B = \frac{{{{10}^2} + {8^2} - {6^2}}}{{2.10.8}} = \frac{4}{5}\\ \Rightarrow \widehat A = {90^o},\widehat B = {36^o}52'11,63''\\ \Rightarrow \widehat C = {53^o}7'48,37''\end{array}\)

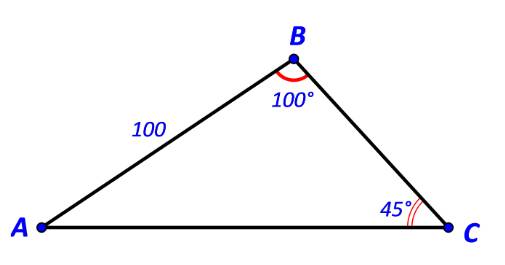
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)

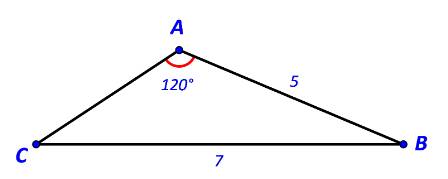
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
\( \Rightarrow \widehat C \approx 38,{2^o}\) hoặc \(\widehat C \approx 141,{8^o}\) (Loại)
Ta có: \(\widehat A = {120^o},\widehat C = 38,{2^o}\)\( \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
Vậy độ dài cạnh AC là 3.

Theo định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\quad (*)\)
+) Ta có: \(\hat A = {180^o} - \left( {\hat B + \;\hat C} \right) = {180^o} - \left( {{{60}^o} + {{45}^o}} \right) = {75^o}\)
\( \Rightarrow a = \frac{b}{{\sin B}}.\sin A = \frac{{10}}{{\sin {{60}^o}}}.\sin {75^o} \approx 11,154\)
+) \((*) \Rightarrow R = \frac{b}{{2\sin B}} = \frac{{10}}{{2\sin {{60}^o}}} = \frac{{10}}{{2.\frac{{\sqrt 3 }}{2}}} = \frac{{10\sqrt 3 }}{3}.\)
+) Diện tích tam giác ABC là: \(S = \frac{1}{2}ab.\sin {\mkern 1mu} \hat C\) \( \approx \frac{1}{2}.11,154.10.\sin {45^o}\)\( \approx 39,44\)
+) Lại có: \(R = \frac{c}{{2\sin C}}\)\( \Rightarrow c = 2.\frac{{10\sqrt 3 }}{3}.\sin {45^o} = \frac{{10\sqrt 6 }}{3} \approx 8,165\)
\( \Rightarrow p = \frac{{a + b + c}}{2} \approx \frac{{11,154 + 10 + 8,165}}{2} \approx 14,66\)
\( \Rightarrow r = \frac{S}{p} \approx \frac{{39,44}}{{14,66}} \approx 2,7\)

Ta có: \(\widehat B = {75^o},\widehat C = {45^o}\)\( \Rightarrow \widehat A = {180^o} - \left( {{{75}^o} + {{45}^o}} \right) = {60^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin {45^o}.\frac{{50}}{{\sin {{60}^o}}} \approx 40,8\)
Vậy độ dài cạnh AB là 40,8.

AB.AC= |AB||AC|.cos(ab,ac)=-35/2
AB.BC=AB(BA+AC)=-49+ -35/2=-133/2

Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{A}=75^o\)
* \(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\Rightarrow AB=\dfrac{BCsinC}{sinA}=a\left(1+\sqrt{3}\right)\)
* \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\Rightarrow AC=\dfrac{BCsinB}{sinA}=a\left(\dfrac{-6+3\sqrt{2}}{2}\right)\)
a) Ta cần tính cạnh BC và hai góc \(\widehat B,\widehat C.\)
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {14^2} + {23^2} - 2.14.23.\cos {125^o}\\ \Rightarrow BC \approx 33\end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{33}}{{\sin {{125}^o}}} = \frac{{23}}{{\sin B}} = \frac{{14}}{{\sin C}}\\ \Rightarrow \sin B = \frac{{23.\sin {{125}^o}}}{{33}} \approx 0,57\\ \Rightarrow \widehat B \approx {35^o} \Rightarrow \widehat C \approx {20^o}\end{array}\)
b) Ta cần tính góc A và hai cạnh AB, AC.
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {64^o} - {38^o} = {78^o}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{22}}{{\sin {{78}^o}}} = \frac{{AC}}{{\sin {{64}^o}}} = \frac{{AB}}{{\sin {{38}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}AC = \sin {64^o}.\frac{{22}}{{\sin {{78}^o}}} \approx 20,22\\AB = \sin {38^o}.\frac{{22}}{{\sin {{78}^o}}} \approx 13,85\end{array} \right.\end{array}\)
c) Ta cần tính góc A và hai cạnh AB, BC.
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {120^o} - {28^o} = {32^o}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{BC}}{{\sin {{32}^o}}} = \frac{{22}}{{\sin {{120}^o}}} = \frac{{AB}}{{\sin {{28}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}BC = \sin {32^o}.\frac{{22}}{{\sin {{120}^o}}} \approx 13,5\\AB = \sin {28^o}.\frac{{22}}{{\sin {{120}^o}}} \approx 12\end{array} \right.\end{array}\)
d) Ta cần tính số đo ba góc \(\widehat A,\widehat B,\widehat C\)
Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2.AB.AC}};\cos B = \frac{{B{C^2} + A{B^2} - A{C^2}}}{{2.BC.BA}}\\ \Rightarrow \cos A = \frac{{{{32}^2} + {{23}^2} - {{44}^2}}}{{2.32.23}} = \frac{{ - 383}}{{1472}};\cos B = \frac{{{{44}^2} + {{23}^2} - {{32}^2}}}{{2.44.23}} = \frac{{131}}{{184}}\\ \Rightarrow \widehat A \approx {105^o},\widehat B = {44^o}36'\\ \Rightarrow \widehat C = {30^o}24'\end{array}\)