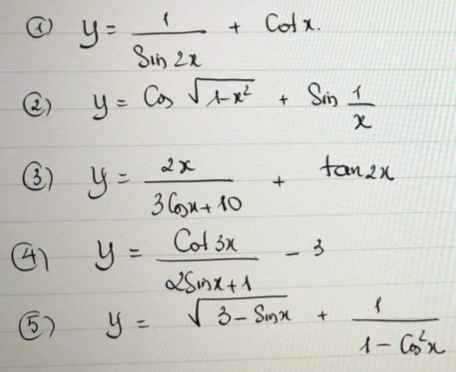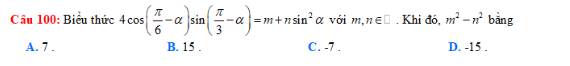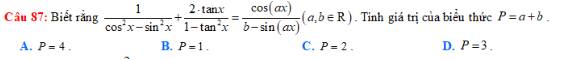Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)

4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7

Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)

ĐK: `x \ne kπ`
`cot(x-π/4)+cot(π/2-x)=0`
`<=>cot(x-π/4)=-cot(π/2-x)`
`<=>cot(x-π/4)=cot(x-π/2)`
`<=> x-π/4=x-π/2+kπ`
`<=>0x=-π/4+kπ` (VN)
Vậy PTVN.

Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF

2.
\(\Leftrightarrow cos2x-cos8x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow2sin5x.sin3x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow sin3x\left(2sin5x-1\right)-cos5x\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left(sin3x-cos5x\right)\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=sin3x=cos\left(\dfrac{\pi}{2}-3x\right)\\sin5x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}-3x+k2\pi\\5x=3x-\dfrac{\pi}{2}+k2\pi\\5x=\dfrac{\pi}{6}+k2\pi\\5x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{k\pi}{4}\\x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{30}+\dfrac{k2\pi}{5}\\x=\dfrac{\pi}{6}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
3.
\(\Leftrightarrow1+sinx=cosx-cos3x+2sinx.cosx+1-2sin^2x\)
\(\Leftrightarrow sinx=2sin2x.sinx+2sinx.cosx-2sin^2x\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\1=2sin2x+2cosx-2sinx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow4sinx.cosx+2cosx-2sinx-1=0\)
\(\Leftrightarrow2cosx\left(2sinx+1\right)-\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2cosx+1\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)