K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MT
2
26 tháng 8 2021
Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF
SM
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
71.
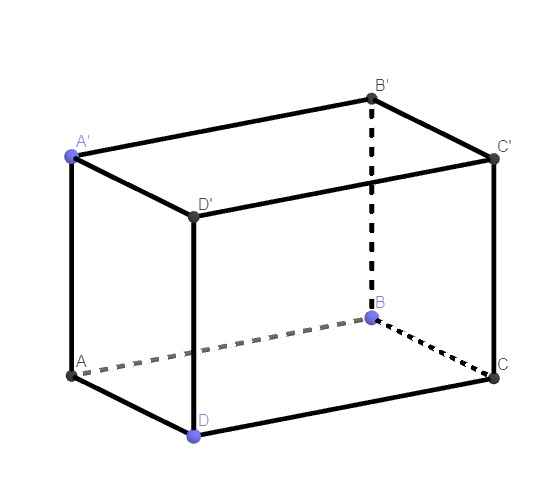
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7
BA
1
20 tháng 7 2023
Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)
F
17 tháng 4 2022
\(y=\dfrac{sinx-cosx}{sinx+cosx}\Rightarrow y'=\dfrac{\left(sinx-cosx\right)'.\left(sinx+cosx\right)-\left(sinx+cosx\right)'.\left(sinx-cosx\right)}{\left(sinx+cosx\right)^2}\)
Dễ thấy : \(\left(sinx-cosx\right)'=cosx+sinx\)
\(\left(sinx+cosx\right)'=cosx-sinx\)
Suy ra : \(y'=\dfrac{\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}=\dfrac{2}{\left(sinx+cosx\right)^2}\)
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
Giả thiết suy ra MN là đường trung bình tam giác ABC \(\Rightarrow MN||BC\)
Mà \(\left\{{}\begin{matrix}MN=\left(DMN\right)\cap\left(ABC\right)\\BC=\left(BCD\right)\cap\left(ABC\right)\end{matrix}\right.\)
Và D là 1 điểm chung của (BCD) và (DMN)
\(\Rightarrow\) Giao tuyến của (BCD) và (DMN) phải là 1 đường thẳng qua D và song song MN (hoặc BC)
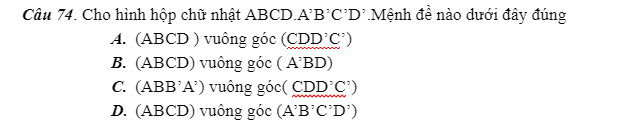
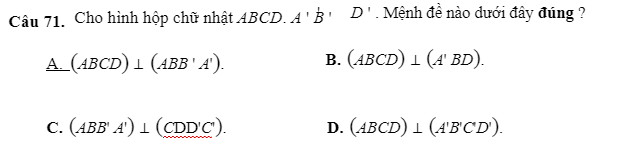
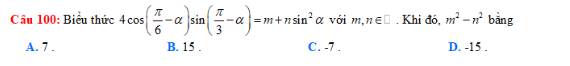
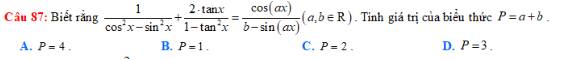
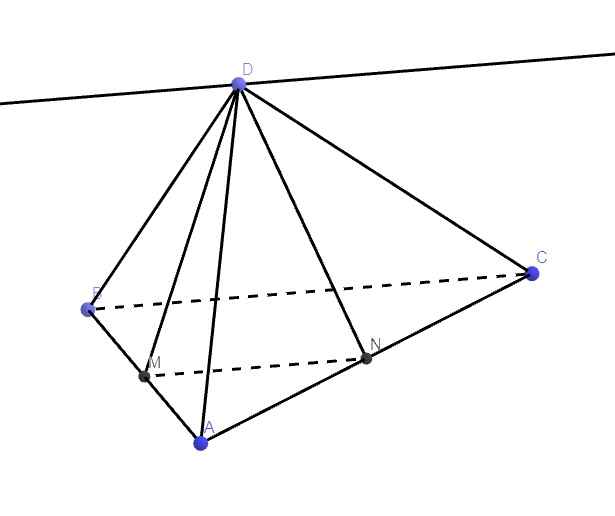
Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)
vẽ hình dùm em luôn ạ
em cảm ơn thầy