Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



M= \(\frac{\sqrt{x}+6}{\sqrt{x}+1}=\frac{5}{\sqrt{x}+1}+1\)
Để M nguyên \(\Leftrightarrow\)\(\frac{5}{\sqrt{x}+1}+1\)nguyên
\(\Leftrightarrow\)\(\frac{5}{\sqrt{x}+1}\)nguyên
\(\Leftrightarrow5⋮\left(\sqrt{x}+1\right)\)\(\Leftrightarrow\)\(\left(\sqrt{x}+1\right)\in\)Ư(5)={1;5;-1;-5}
Ta có bảng :
| \(\sqrt{x}+1\) | -5 | -1 | 1 | 5 |
| \(x\) | ko có giá trị thỏa mãn | ko có giá trị thỏa mãn | 0 | 2 |
Vậy các số hữu tỉ a thõa mãn là (0 ;2 )

Lời giải:
a.
Áp dụng BĐT Bunhiacopxky:
$A^2=(\sqrt{x-1}+\sqrt{9-x})^2\leq (x-1+9-x)(1+1)=16$
$\Rightarrow A\leq 4$
Vậy $A_{\max}=4$. Giá trị này đạt tại $x=5$
b.
$A=\frac{3(\sqrt{x}+2)+5}{\sqrt{x}+2}=3+\frac{5}{\sqrt{x}+2}$
Để $A$ nguyên thì $\frac{5}{\sqrt{x}+2}=m$ với $m$ nguyên dương
$\Leftrightarrow \sqrt{x}+2=\frac{5}{m}$
$\sqrt{x}=\frac{5-2m}{m}$
Vì $\sqrt{x}\geq 0$ nên $\frac{5-2m}{m}\geq 0$
Mà $m$ nguyên dương nên $5-2m\geq 0$
$\Leftrightarrow m\leq 2,5$.
$\Rightarrow m=1; 2$
$\Rightarrow x=9; x=\frac{1}{4}$

Ta có \(M=\frac{\sqrt{a}+2}{\sqrt{a}-2}=\frac{\sqrt{a}-2}{\sqrt{a}-2}+\frac{4}{\sqrt{a}-2}=1+\frac{4}{\sqrt{a}-2}\)
Để M nguyên thì \(\frac{4}{\sqrt{a}-2}\)nguyên
Ta có bảng sau:
| \(\sqrt{a}\)-2 | 1 | -1 | 2 | -2 | 4 | -4 |
| a | Loại | 1 | 16 | 0 | Loại | Loại |
Vậy tại a là 0;16;2 thì M nguyên


Bài 8:
\(M=1+\frac{4}{\sqrt{x}+1}\)
Để $M$ nguyên thì $\frac{4}{\sqrt{x}+1}$ nguyên
Đặt $\frac{4}{\sqrt{x}+1}=t$ với $t$ là số nguyên dương
$\Rightarrow \sqrt{x}+1=\frac{4}{t}$
$\sqrt{x}=\frac{4}{t}-1=\frac{4-t}{t}\geq 0$
$\Rightarrow 4-t\geq 0\Rightarrow t\leq 4$
Mà $t$ nguyên dương suy ra $t=1;2;3;4$
Kéo theo $x=9; 1; \frac{1}{9}; 0$
Kết hợp đkxđ nên $x=0; \frac{1}{9};9$
Bài 9:
$P=1+\frac{5}{\sqrt{x}+2}$
Để $P$ nguyên thì $\frac{5}{\sqrt{x}+2}$ nguyên
Đặt $\frac{5}{\sqrt{x}+2}=t$ với $t\in\mathbb{Z}^+$
$\Leftrightarrow \sqrt{x}+2=\frac{5}{t}$
$\Leftrightarrow \sqrt{x}=\frac{5-2t}{t}\geq 0$
Với $t>0\Rightarrow 5-2t\geq 0$
$\Leftrightarrow t\leq \frac{5}{2}$
Vì $t$ nguyên dương suy ra $t=1;2$
$\Rightarrow x=9; \frac{1}{4}$ (thỏa đkxđ)
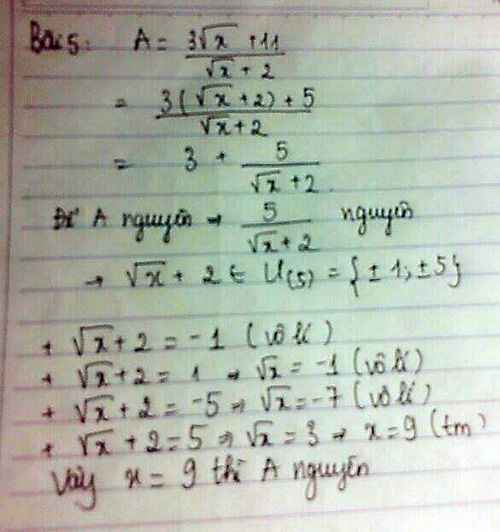
Ta có : \(M=\frac{\sqrt{x}+6}{\sqrt{x}+1}=\frac{\sqrt{x}+1+5}{\sqrt{x}+1}=\frac{\sqrt{x}+1}{\sqrt{x}+1}+\frac{5}{\sqrt{x}+1}=1+\frac{5}{\sqrt{x}+1}\)
Để M nguyên thì 5 chia hết cho \(\sqrt{x}+1\)
Nên : \(\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Ta có bảng :
bài có nhầm đề không bạn? vì tử = mẫu thì M=1 rồi kìa