
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(-x+80=-220-5x\)
\(\Rightarrow-x+5x=-220-80\)
\(\Rightarrow4x=-300\)
\(\Rightarrow x=-\dfrac{300}{4}\)
\(\Rightarrow x=-75\)
b) \(98+\left(x-12\right)+68=-80-x\)
\(\Rightarrow166+\left(x-12\right)=-80-x\)
\(\Rightarrow166+x-12=-80-x\)
\(\Rightarrow154+x=-80-x\)
\(\Rightarrow154+80=-x-x\)
\(\Rightarrow-2x=234\)
\(\Rightarrow x=-\dfrac{234}{2}\)
\(\Rightarrow x=-117\)
c) \(122+x-78=-55-4x-1\)
\(\Rightarrow44+x=-56-4x\)
\(\Rightarrow x+4x=-56-44\)
\(\Rightarrow5x=-100\)
\(\Rightarrow x=-\dfrac{100}{5}\)
\(\Rightarrow x=-20\)
d) \(663+9x=-x-37\)
\(\Rightarrow9x+x=-37-663\)
\(\Rightarrow10x=-700\)
\(\Rightarrow x=-\dfrac{700}{10}\)
\(\Rightarrow x=-70\)

a) \(-\left(-a+c-d\right)-\left(c-a+d\right)\)
\(=a-c+d-c+a-d\)
\(=2a-2c\)
b) \(-\left(a+b-c+d\right)+\left(a-b-c-d\right)\)
\(=-a-b+c-d+a-b-c-d\)
\(=-2b-2d\)
c) \(a\left(b-c-d\right)-a\left(b+c-d\right)\)
\(=ab-ac-ad-ab-ac+ad\)
\(=-2ac\)
d) \(\left(a-b\right)+\left(c-d\right)+\left(a+c\right)-\left(b+d\right)\)
\(=a-b+c-d+a+c-b-d\)
\(=2a-2b+2c-2d\)

h) \(\left(a-b\right)-\left(c-d\right)-\left(a+d\right)-\left(b+c\right)\)
\(=a-b-c+d-a-d-b-c\)
\(=\left(a-a\right)-\left(b+b\right)-\left(c+c\right)+\left(d+d\right)\)
\(=-2b-2c\)
i) \(-\left(-a+c-d\right)-\left(c-a+d\right)\)
\(=a-c+d-c+a-d\)
\(=\left(a+a\right)-\left(c+c\right)+\left(d+d\right)\)
\(=2a-2c\)
k) \(-\left(a+b-c+d\right)+\left(a-b-c-d\right)\)
\(=-a-b+c-d+a-b-c-d\)
\(=\left(-a+a\right)-\left(b+b\right)+\left(c-c\right)-\left(d+d\right)\)
\(=-2b-2d\)
n) \(-a\left(-b-c+d-e\right)-\left(-a\right)-\left(-b+c-d\right)\)
\(=ab+ac-ad+ae+a+b-c+d\)

\(\left(x-2\right)^7=\left(x-2\right)^5\)
\(\Leftrightarrow\left(x-2\right)^7-\left(x-2\right)^5=0\)
\(\Leftrightarrow\left(x-2\right)^5.\left[\left(x-2\right)^2-1\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-2\right)^5=0\\\left(x-2\right)^2-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3;x=1\end{cases}}}\)
Vậy \(x\in\left\{1;-1;2\right\}\)
:V sửa lại hộ mình cái kết luận nhé
\(x\in\left\{-1;3;2\right\}\)

Bài làm
\(\frac{1}{100.99}-\frac{1}{99.98}-\frac{1}{98.97}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
=\(\left(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{98.99}+\frac{1}{99.100}\right)\)
=\(\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{98}-\frac{1}{99}+\frac{1}{99}-\frac{1}{100}\right)\)
=\(\left(1-\frac{1}{100}\right)\)
=\(\left(\frac{100}{100}-\frac{1}{100}\right)\)
=\(\frac{99}{100}\)
Chúc bạn học tốt

Bài 11:
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{20}}\)
=>\(3\cdot A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}\)
=>\(3\cdot A-A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{19}}-\dfrac{1}{3^{20}}\)
=>\(2A=1-\dfrac{1}{3^{20}}=\dfrac{3^{20}-1}{3^{20}}\)
=>\(A=\dfrac{3^{20}-1}{2\cdot3^{20}}\)
Bài 6:
a: ĐKXĐ: x>=-2
\(\sqrt{x+2}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(\sqrt{x+2}+2>=2\forall x\) thỏa mãn ĐKXĐ
=>\(A>=2\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+2=0
=>x=-2
Vậy: \(A_{min}=2\) khi x=-2
b: ĐKXĐ: x>=-5
\(\sqrt{x+5}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(5\sqrt{x+5}>=0\forall x\)thỏa mãn ĐKXĐ
=>\(5\sqrt{x+5}-\dfrac{3}{5}>=-\dfrac{3}{5}\forall x\) thỏa mãn ĐKXĐ
=>\(B>=-\dfrac{3}{5}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+5=0
=>x=-5
vậy: \(B_{min}=-\dfrac{3}{5}\) khi x=-5

\(n,3.4^x-2^{2x+1}=16\\ \Leftrightarrow3.4^x-4^x.2=2^4\\ \Leftrightarrow4^x=4^2\\ \Leftrightarrow x=2\)
\(m,5.3^{x-1}+3^{x+1}=52\\ \Leftrightarrow\dfrac{5}{3}.3^x+3.3^x=52\\ \Leftrightarrow\dfrac{14}{3}.3^x=52\\ \Leftrightarrow3^x=\dfrac{78}{7}\)
đến đây ko bt
 lm từng bước giúp mk nhé, cảm ơn
lm từng bước giúp mk nhé, cảm ơn

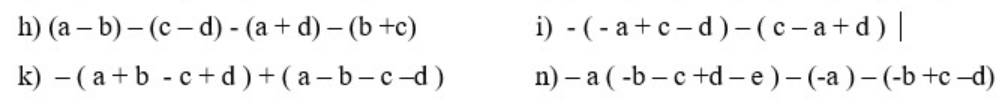
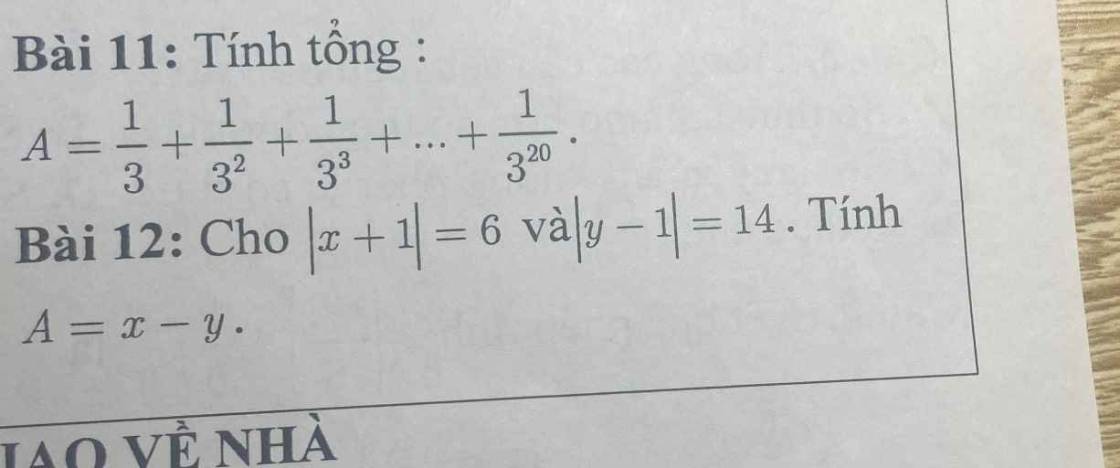
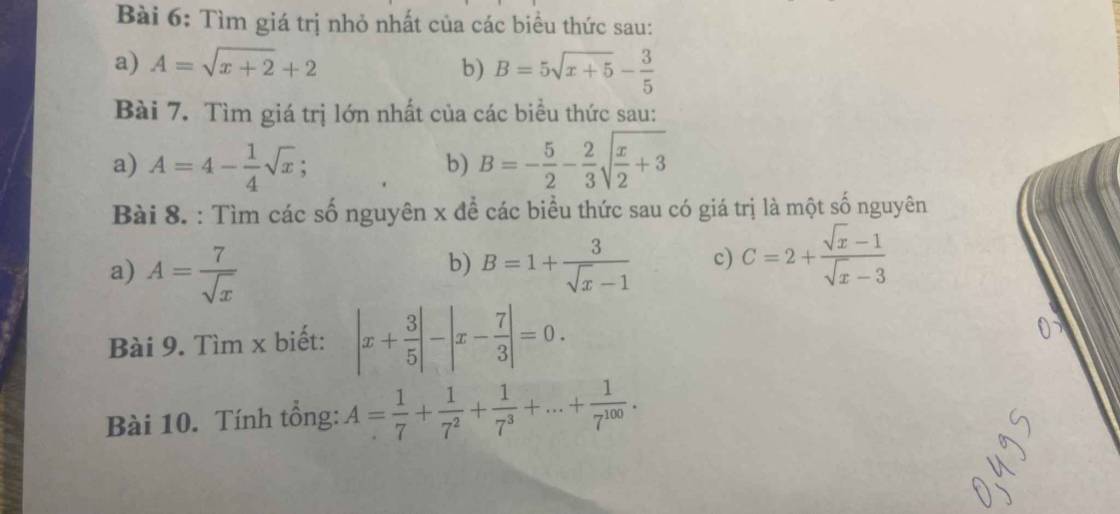
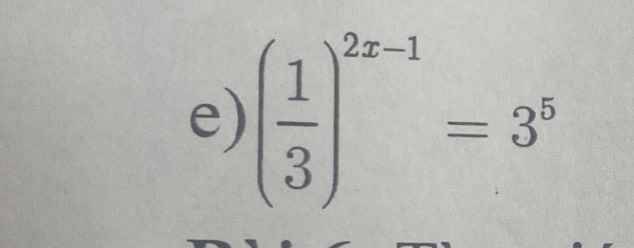
 giúp mk vs, cảm ơn trc (lm 1 câu thôi cngx đc)
giúp mk vs, cảm ơn trc (lm 1 câu thôi cngx đc)
a) \(\left(2x-4\right)\left(x-2\right)^3=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-4=0\\\left(x-2\right)^3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=4\\x-2-0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=2\end{matrix}\right.\)
\(\Rightarrow x=2\)
b) \(3^{x-1}:81=3^3\)
\(\Rightarrow3^{x-1}:3^4=3^3\)
\(\Rightarrow3^{x-1-4}=3^3\)
\(\Rightarrow3^{x-5}=3^3\)
\(\Rightarrow x-5=3\)
\(\Rightarrow x=8\)
c) \(x^{13}=x\)
\(\Rightarrow x^{13}-x=0\)
\(\Rightarrow x\left(x^{12}-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^{12}-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^{12}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
d) \(\left(x-9\right)^4=\left(x-9\right)^2\)
\(\Rightarrow\left(x-9\right)^2=x-9\)
\(\Rightarrow\left(x-9\right)^2-\left(x-9\right)=0\)
\(\Rightarrow\left(x-9\right)\left(x-9-1\right)=0\)
\(\Rightarrow\left(x-9\right)\left(x-10\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-9=0\\x-10=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=9\\x=10\end{matrix}\right.\)