
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5B:
a: Xét ΔABC và ΔEBF có
BA=BE
\(\widehat{ABC}=\widehat{EBF}\)
BC=BF
Do đó: ΔABC=ΔEBF
b: ΔABC=ΔEBF
=>\(\widehat{BAC}=\widehat{BEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//EF
Xét tứ giác ACEF có
B là trung điểm chung của AE và CF
Do đó: ACEF là hình bình hành
=>AF//CE
c: Xét tứ giác AMEN có
AM//EN
AM=EN
Do đó: AMEN là hình bình hành
=>AE cắt MN tại trung điểm của mỗi đường
mà B là trung điểm của AE
nên B là trung điểm của MN
=>M,B,N thẳng hàng

Bài 3:
a: Đặt \(\widehat{B}=b;\widehat{C}=c\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(b+c+80^0=180^0\)
=>\(b+c=100^0\)
mà b-c=20
nên \(\left\{{}\begin{matrix}b=\dfrac{100+20}{2}=60\\c=60-20=40\end{matrix}\right.\)
Vậy: \(\widehat{B}=60^0;\widehat{C}=40^0\)
b: AD là phân giác của \(\widehat{BAC}\)
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot80^0=40^0\)
Xét ΔADC có \(\widehat{ADB}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{DAC}+\widehat{C}\)
=>\(\widehat{ADB}=40^0+40^0=80^0\)
4:
a: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{BAC}+20^0+40^0=180^0\)
=>\(\widehat{BAC}=120^0\)
=>ΔABC là tam giác tù
b: AD nằm giữa AB và AC
=>\(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=120^0\)
mà \(\widehat{CAD}=2\cdot\widehat{BAD}\)
nên \(\widehat{CAD}=\dfrac{2}{3}\cdot120^0=80^0\)
=>\(\widehat{BAD}=\dfrac{1}{2}\cdot80^0=40^0\)
Xét ΔABD có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{BAD}+\widehat{B}=40^0+20^0=60^0\)

Bài 3:
1, Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{z-x}{3-6}=\dfrac{-21}{-3}=7\\ \Rightarrow\left\{{}\begin{matrix}x=42\\y=28\\z=21\end{matrix}\right.\)
2, Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{2x+3y-z}{6+15-7}=\dfrac{-14}{14}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-3\\y=-5\\z=-7\end{matrix}\right.\)
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+y+z}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{130}{\dfrac{13}{12}}=120\)
Do đó: x=60; y=40; z=30

12300 nha , e ms hc lp 6 thoy hà !!!!!!!!!!! Avatar của cj là ak mak cute zậy

\(\left|3x+2\right|=\left|4x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=4x-3\\3x+2=3-4x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=-5\\7x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{7}\end{matrix}\right.\)
\(\left|2+3x\right|=\left|4x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2+3x=4x-3\\2+3x=3-4x\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{7}\end{matrix}\right.\)
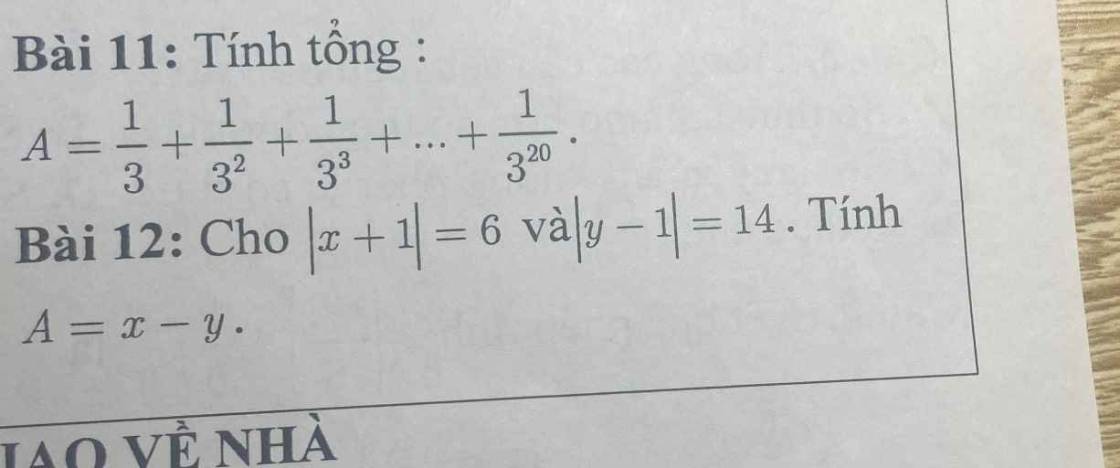
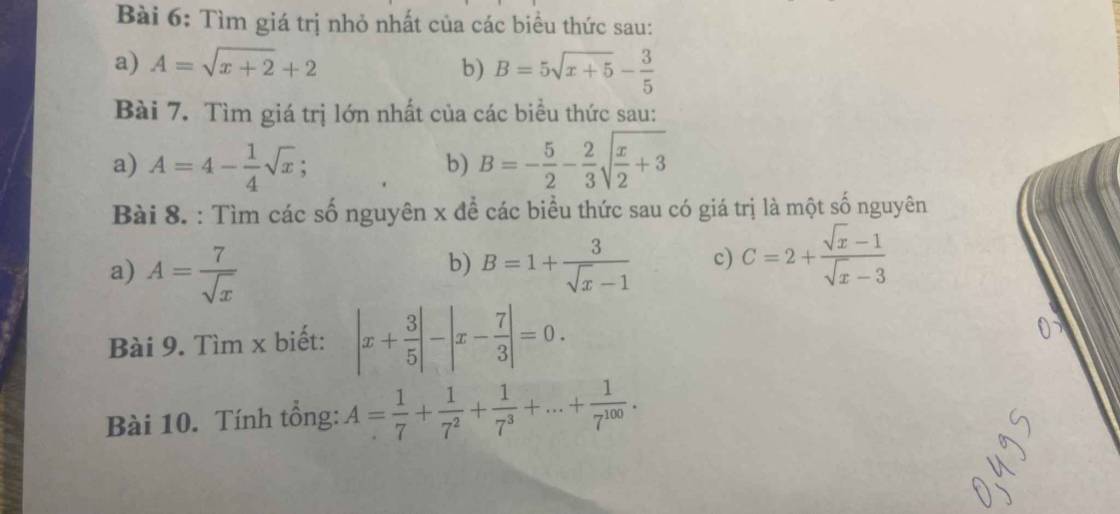
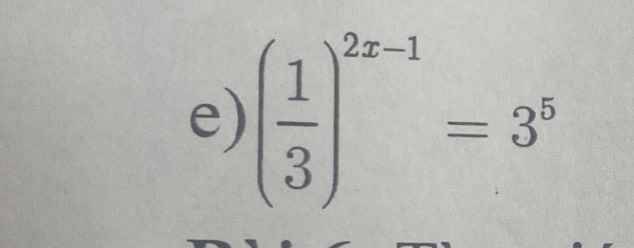


 lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
Bài 11:
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{20}}\)
=>\(3\cdot A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}\)
=>\(3\cdot A-A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{19}}-\dfrac{1}{3^{20}}\)
=>\(2A=1-\dfrac{1}{3^{20}}=\dfrac{3^{20}-1}{3^{20}}\)
=>\(A=\dfrac{3^{20}-1}{2\cdot3^{20}}\)
Bài 6:
a: ĐKXĐ: x>=-2
\(\sqrt{x+2}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(\sqrt{x+2}+2>=2\forall x\) thỏa mãn ĐKXĐ
=>\(A>=2\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+2=0
=>x=-2
Vậy: \(A_{min}=2\) khi x=-2
b: ĐKXĐ: x>=-5
\(\sqrt{x+5}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(5\sqrt{x+5}>=0\forall x\)thỏa mãn ĐKXĐ
=>\(5\sqrt{x+5}-\dfrac{3}{5}>=-\dfrac{3}{5}\forall x\) thỏa mãn ĐKXĐ
=>\(B>=-\dfrac{3}{5}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+5=0
=>x=-5
vậy: \(B_{min}=-\dfrac{3}{5}\) khi x=-5