
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Đặt \(\widehat{B}=b;\widehat{C}=c\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(b+c+80^0=180^0\)
=>\(b+c=100^0\)
mà b-c=20
nên \(\left\{{}\begin{matrix}b=\dfrac{100+20}{2}=60\\c=60-20=40\end{matrix}\right.\)
Vậy: \(\widehat{B}=60^0;\widehat{C}=40^0\)
b: AD là phân giác của \(\widehat{BAC}\)
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot80^0=40^0\)
Xét ΔADC có \(\widehat{ADB}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{DAC}+\widehat{C}\)
=>\(\widehat{ADB}=40^0+40^0=80^0\)
4:
a: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{BAC}+20^0+40^0=180^0\)
=>\(\widehat{BAC}=120^0\)
=>ΔABC là tam giác tù
b: AD nằm giữa AB và AC
=>\(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=120^0\)
mà \(\widehat{CAD}=2\cdot\widehat{BAD}\)
nên \(\widehat{CAD}=\dfrac{2}{3}\cdot120^0=80^0\)
=>\(\widehat{BAD}=\dfrac{1}{2}\cdot80^0=40^0\)
Xét ΔABD có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{BAD}+\widehat{B}=40^0+20^0=60^0\)

Bài 11:
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{20}}\)
=>\(3\cdot A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}\)
=>\(3\cdot A-A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{19}}-\dfrac{1}{3^{20}}\)
=>\(2A=1-\dfrac{1}{3^{20}}=\dfrac{3^{20}-1}{3^{20}}\)
=>\(A=\dfrac{3^{20}-1}{2\cdot3^{20}}\)
Bài 6:
a: ĐKXĐ: x>=-2
\(\sqrt{x+2}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(\sqrt{x+2}+2>=2\forall x\) thỏa mãn ĐKXĐ
=>\(A>=2\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+2=0
=>x=-2
Vậy: \(A_{min}=2\) khi x=-2
b: ĐKXĐ: x>=-5
\(\sqrt{x+5}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(5\sqrt{x+5}>=0\forall x\)thỏa mãn ĐKXĐ
=>\(5\sqrt{x+5}-\dfrac{3}{5}>=-\dfrac{3}{5}\forall x\) thỏa mãn ĐKXĐ
=>\(B>=-\dfrac{3}{5}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+5=0
=>x=-5
vậy: \(B_{min}=-\dfrac{3}{5}\) khi x=-5

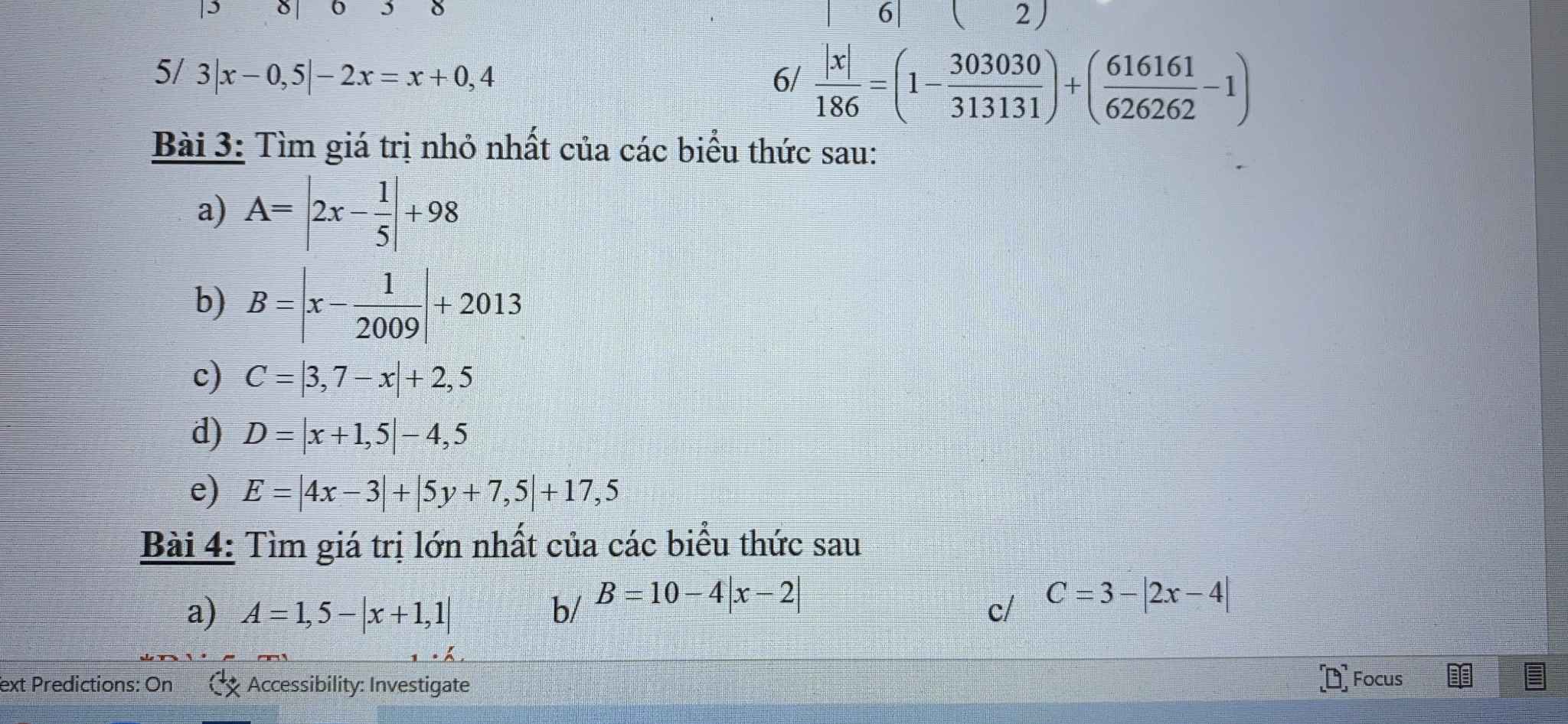
Bài 4:
a: Ta có: \(-\left|x+1.1\right|\le0\forall x\)
\(\Leftrightarrow-\left|x+1.1\right|+1.5\le1.5\forall x\)
Dấu '=' xảy ra khi x=-1,1
b: Ta có: \(-4\left|x-2\right|\le0\forall x\)
\(\Leftrightarrow-4\left|x-2\right|+10\le10\forall x\)
Dấu '=' xảy ra khi x=2

Bài 4:
a: \(4x=3y\)
=>\(\dfrac{x}{3}=\dfrac{y}{4}=k\)
=>x=3k; y=4k
\(\left(x-y\right)^2+\left(x+y\right)^2=50\)
=>\(\left(3k-4k\right)^2+\left(3k+4k\right)^2=50\)
=>\(\left(-k\right)^2+\left(7k\right)^2=50\)
=>\(50k^2=50\)
=>\(k^2=1\)
TH1: k=1
=>\(x=3\cdot1=3;y=4\cdot1=4\)
TH2: k=-1
=>\(x=3\cdot\left(-1\right)=-3;y=4\cdot\left(-1\right)=-4\)
b: 3x=2y
=>\(\dfrac{x}{2}=\dfrac{y}{3}=k\)
=>x=2k; y=3k
\(\left(x+y\right)^3-\left(x-y\right)^3=126\)
=>\(\left(2k+3k\right)^3-\left(2k-3k\right)^3=126\)
=>\(\left(5k\right)^3-\left(-k\right)^3=126\)
=>\(126k^3=126\)
=>\(k^3=1\)
=>k=1
=>\(x=2\cdot1=2;y=3\cdot1=3\)
bài 3:
a: \(\dfrac{x}{2}=\dfrac{y}{5}\)
=>\(\dfrac{x}{6}=\dfrac{y}{15}\left(1\right)\)
\(\dfrac{y}{3}=\dfrac{z}{2}\)
=>\(\dfrac{y}{15}=\dfrac{z}{10}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{10}\)
mà 2x+3y-4z=34
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{10}=\dfrac{2x+3y-4z}{2\cdot6+3\cdot15-4\cdot10}=\dfrac{34}{12+45-40}=2\)
=>\(x=2\cdot6=12;y=2\cdot15=30;z=2\cdot10=20\)
b: 2x=3y
=>\(\dfrac{x}{3}=\dfrac{y}{2}\)
=>\(\dfrac{x}{21}=\dfrac{y}{14}\left(3\right)\)
5y=7z
=>\(\dfrac{y}{7}=\dfrac{z}{5}\)
=>\(\dfrac{y}{14}=\dfrac{z}{10}\left(4\right)\)
Từ (3),(4) suy ra \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)
mà 3x-7y+5z=30
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}=\dfrac{3x-7y+5z}{3\cdot21-7\cdot14+5\cdot10}=\dfrac{30}{63-98+50}=\dfrac{30}{113-98}=2\)
=>\(x=2\cdot21=42;y=2\cdot14=28;z=2\cdot10=20\)

Bài 2:
a: Xét ΔABD có AD<AB+BD(BĐT tam giác)
b: Xét ΔACD có AD<AC+CD(BĐT tam giác)
ta có: AD<AB+BD
AD<AC+CD
Do đó: AD+AD<AB+BD+AC+CD
=>2AD<AB+AC+BC
c: \(2AD< AB+AC+BC\)
=>\(AD< \dfrac{1}{2}\left(AB+AC+BC\right)\)
=>\(AD< \dfrac{1}{2}\cdot C_{ABC}\)
Bài 11:
a: ΔMDN vuông tại D
=>MN là cạnh huyền
=>MN là cạnh lớn nhất trong ΔMDN
=>MN>MD
b: Ta có: ΔMEN vuông tại E
=>MN là cạnh huyền của ΔMEN
=>MN là cạnh lớn nhất trong ΔMEN
=>MN>NE
mà MN>MD
nên MN+MN>MD+NE
=>2MN>MD+NE


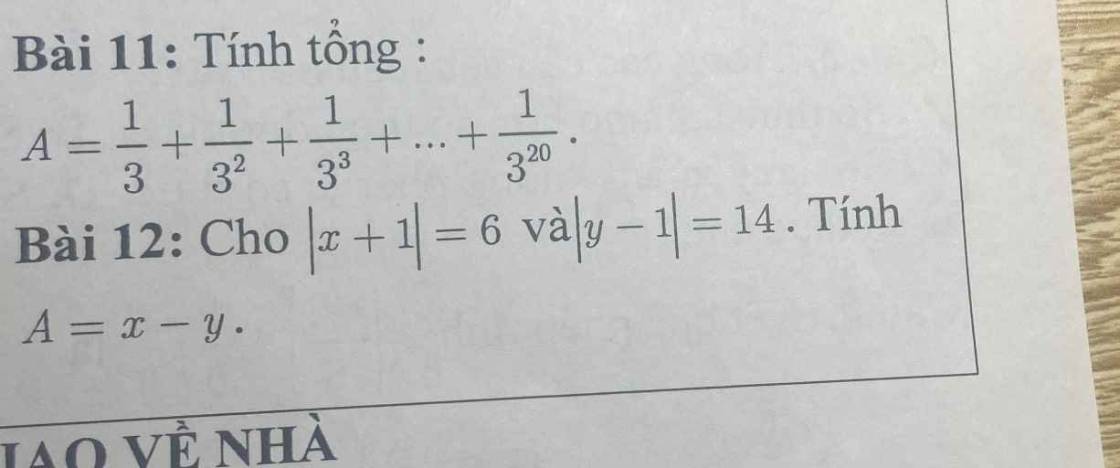
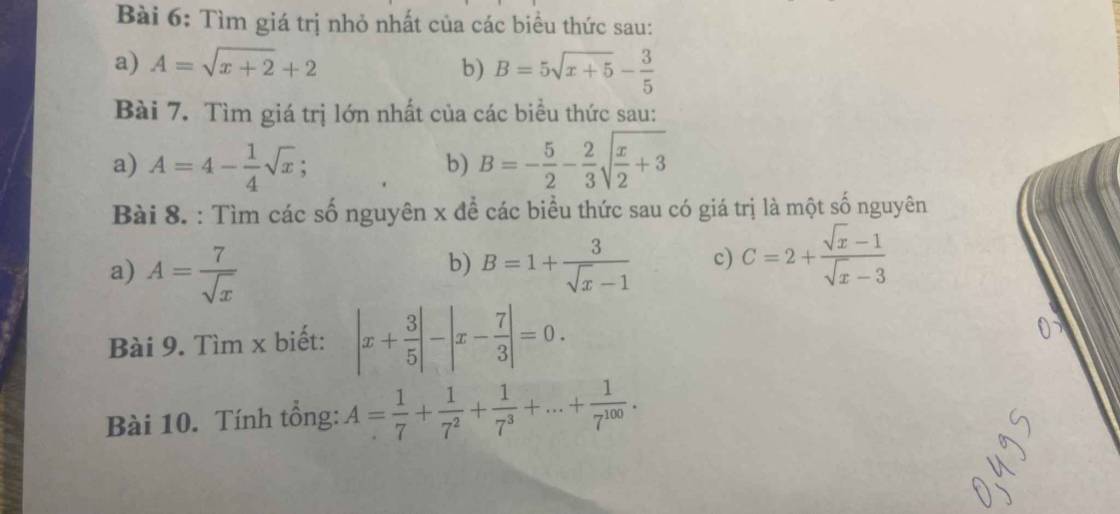
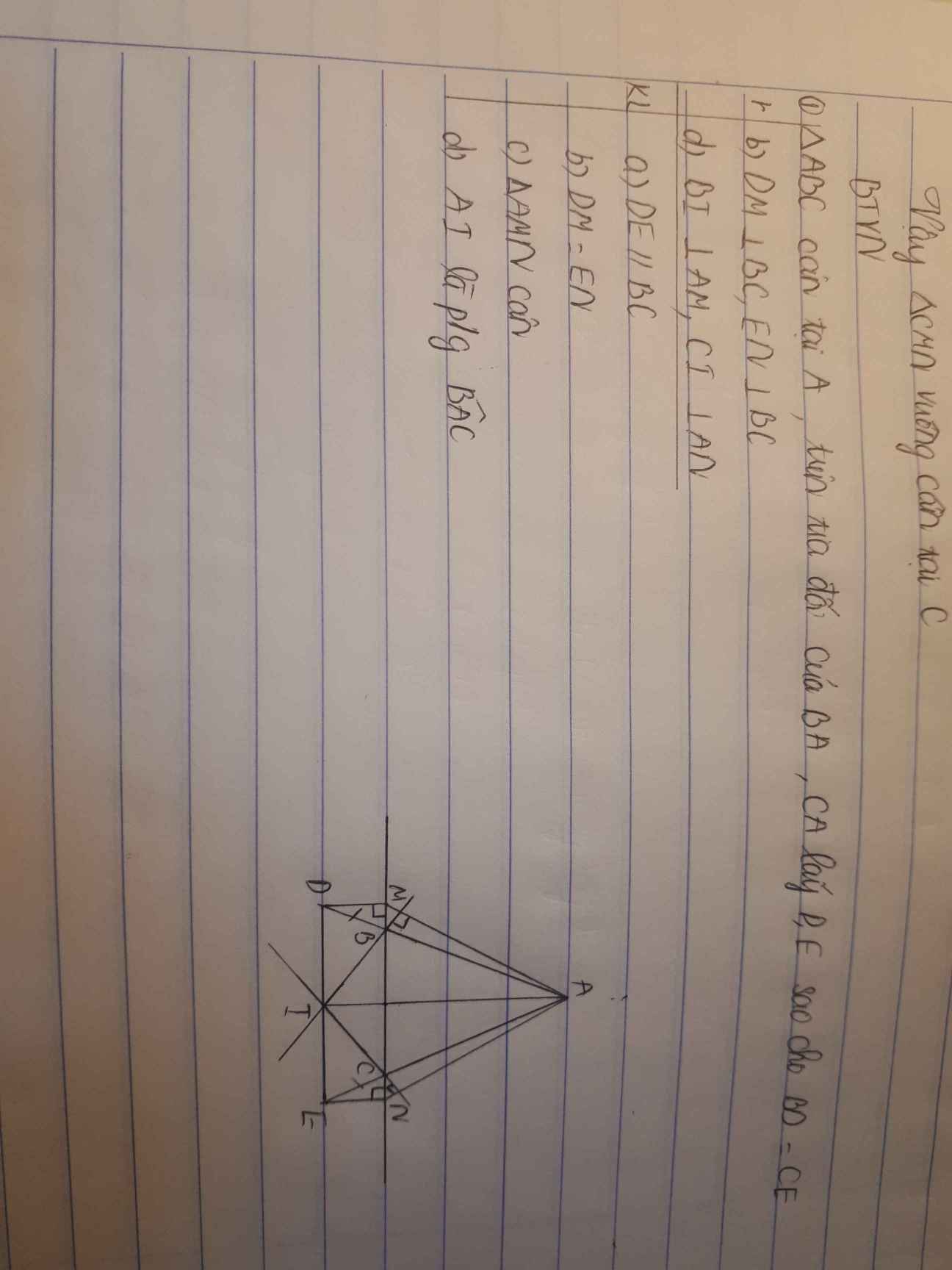


5B:
a: Xét ΔABC và ΔEBF có
BA=BE
\(\widehat{ABC}=\widehat{EBF}\)
BC=BF
Do đó: ΔABC=ΔEBF
b: ΔABC=ΔEBF
=>\(\widehat{BAC}=\widehat{BEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//EF
Xét tứ giác ACEF có
B là trung điểm chung của AE và CF
Do đó: ACEF là hình bình hành
=>AF//CE
c: Xét tứ giác AMEN có
AM//EN
AM=EN
Do đó: AMEN là hình bình hành
=>AE cắt MN tại trung điểm của mỗi đường
mà B là trung điểm của AE
nên B là trung điểm của MN
=>M,B,N thẳng hàng