
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(\left(2x+3\right)^2=4x^2+12x+9\)
\(\left(3x+2\right)^2=9x^2+12x+4\)
\(\left(2x+5\right)^2=4x^2+20x+25\)
\(\left(2x+\dfrac{1}{3}\right)^2=4x^2+\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x+\dfrac{1}{3}\right)^2=9x^2+2x+\dfrac{1}{9}\)
2) \(\left(2x-3\right)^2=4x^2-12x+9\)
\(\left(3x-2\right)^2=9x^2-12x+4\)
\(\left(2x-5\right)^2=4x^2-20x+25\)
\(\left(2x-\dfrac{1}{3}\right)^2=4x^2-\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x-\dfrac{1}{3}\right)^2=9x^2-2x+\dfrac{1}{9}\)
3) \(\left(2x-3\right)\left(2x+3\right)=4x^2-9\)
\(\left(3x-4\right)\left(3x+4\right)=9x^2-16\)
\(\left(2x-5\right)\left(2x+5\right)=4x^2-25\)
\(\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)=x^2-\dfrac{1}{4}\)
\(\left(2x-\dfrac{1}{3}\right)\left(2x+\dfrac{1}{3}\right)=4x^2-\dfrac{1}{9}\)
1: \(\left(2x+3\right)^2=4x^2+12x+9\)
\(\left(3x+2\right)^2=9x^2+12x+4\)
\(\left(2x+5\right)^2=4x^2+20x+25\)
\(\left(2x+\dfrac{1}{3}\right)^2=4x^2+\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x+\dfrac{1}{3}\right)^2=9x^2+2x+\dfrac{1}{9}\)

a, Xét tứ giác ADHE có ^ADH = ^AEH = ^DAE = 900
=> tứ giác ADHE là hcn
=> AH = DE (2 đường chéo bằng nhau)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA = 900
^HAB = ^HCA ( cùng phụ ^HAC )
Vậy tam giác AHB~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=BH.CH\)
c, Xét tam giác AHD và tam giác ABH có
^ADH = ^AHB = 900
^A _ chung
Vậy tam giác AHD ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AD}{AH}\Rightarrow AH^2=AD.AB\)(1)
tương tự tam giác AEH ~ tam giác AHC (g.g)
\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AE.AC\left(2\right)\)
Từ (1) ; (2) suy ra \(AD.AB=AE.AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét tam giác ADE và tam giác ACB
^A _ chung
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\left(cmt\right)\)
Vậy tam giác ADE ~ tam giác ACB (c.g.c)


\(5x^2+10xy-4x-8y\)
\(=5x\left(x+2y\right)-4\left(x+2y\right)\)
\(=\left(x+2y\right)\left(5x-4\right)\)

Lời giải:
a.
$=(5x^2+5xy)+(10x+10y)=5x(x+y)+10(x+y)$
$=(x+y)(5x+10)=5(x+y)(x+2)$
b. Biểu thức không phân tích được thành nhân tử.

a/
\(\widehat{BAE}+\widehat{DAE}=\widehat{BAD}=90^o\)
\(\widehat{DAF}+\widehat{DAE}=\widehat{FAE}=90^o\)
\(\Rightarrow\widehat{BAE}=\widehat{DAF}\) (cùng phụ với \(\widehat{DAE}\) ) (1)
\(AB=AD\) (cạnh hình vuông) (2)
Xét tg vuông ABE và tg vuông ADF
Từ (1) và (2) => tg ABE = tg ADF (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)
\(\Rightarrow AE=AF\) (đpcm)
b/
AE=AF (cmt) => tg AEF là tg cân tại A
I là trung điểm EF (gt)
=> AI là trung tuyến thuộc EF => \(AI\perp EF\) (tring tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)
\(\Rightarrow GK\perp EF\) (3)
Xét tg EIG và tg FIK có
\(\widehat{EIG}=\widehat{FIK}\) (góc đối đỉnh) (4)
EG//AB; AB//CD => EG//CD => EG//FK (5)
\(\Rightarrow\widehat{GEI}=\widehat{KFI}\) (góc so le trong) (6)
\(IE=IF\) (gt) (7)
Từ (4) (6) (7) => tg EIG = tg FIK (g.c.g) => EG = FK (8)
Từ (5) và (8) => EGFK là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau là hình bình hành) (9)
Từ (3) và (9) => EGFK là hình thoi (hình bình hành có hai đường chéo vuông góc với nhau là hình thoi) (đpcm)
c/
Ta có tg AEF cân tại A (cmt); AI là trung tuyến thuộc EF (cmt)
=> AI là phân giác \(\widehat{EAF}\) (trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh)
Mà \(\widehat{EAF}=90^o\)
\(\Rightarrow\widehat{FAK}=45^o\)
\(\widehat{ACF}=45^o\)
\(\Rightarrow\widehat{FAK}=\widehat{ACF}=45^o\)
Xét tg AKF và tg ACF có
\(\widehat{FAK}=\widehat{ACF}=45^o\)
\(\widehat{AFC}\) chung
=> tg AKF đồng dạng với tg CAF (g.g.g)
d/

\(1,\Leftrightarrow x^2-8x+16-x^2+x+12=7\\ \Leftrightarrow-7x=-21\\ \Leftrightarrow x=3\\ 2,\Leftrightarrow\left(x-4\right)^2-\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)

a: Xét ΔBAC có BI/BA=BE/BC
nên EI//AC và EI=1/2AC
=>EI vuông góc AB
DE vuông góc AB tại trung điểm của DE
=>D đối xứng E qua AB
b: Xét tứ giác DECA co
DE//CA
DE=CA(=2EI)
Do đó: DECA là hình bình hành
c: Xét tứ giác ADBE có
I là trung điểm chung của AB và DE
EA=EB
=>ADBE là hình thoi
e: Để ADBE là hình vuông thì góc AEB=90 độ
=>góc ABC=45 độ
Bạn tự vẽ hình nhé.
a) Do \(E\) đối xứng với \(D\) qua \(I\), do đó \(I\) là trung điểm của \(DE\) hay \(ID=IE\).
Ta cũng có : \(E\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AB\) ⇒ \(IE\) là đường trung bình của \(\Delta ABC\) ⇒ \(IE // AC\). Lại có : \(AB\perp AC\) (giả thiết), vì vậy, \(IE\perp AB\).
Từ đó, suy ra \(AB\) là đường trung trực của \(DE\) hay \(D\) đối xứng với \(E\) qua \(AB\) (điều phải chứng minh).
b) Do \(IE\) là đường trung bình của \(\Delta ABC\) (chứng minh trên) nên \(IE=\dfrac{1}{2}AC\) và \(IE//AC\). Mặt khác, \(IE=\dfrac{1}{2}DE\). Suy ra được \(\dfrac{1}{2}AC=\dfrac{1}{2}DE\) hay \(AC=DE\). Suy ra, \(ADEC\) là hình bình hành (điều phải chứng minh).
c) Do \(I\) là trung điểm của \(DE\) (chứng minh trên) và của \(AB\) (giả thiết), suy ra \(ADBE\) là hình bình hành. Lại có \(AB\perp DE\) (do \(AB\) là đường trung trực của \(DE\) (chứng minh trên)). Suy ra, \(ADBE\) là hình thoi.
Do \(ADBE\) là hình thoi nên \(AE=EB=BD=DA=10(cm)\). Do đó, chu vi của hình thoi \(ADBE\) là \(C=AE+EB+BD+DA=4AE=4.10=40\left(cm\right)\).
d) Để hình thoi \(ADBE\) là hình vuông thì \(\hat{E}=90^o\) hay \(AE\) là đường cao của \(\Delta ABC\). Mà \(AE\) lại là đường trung tuyến của \(\Delta ABC\) (do \(E\) là trung điểm của \(BC\)). Để điều đó xảy ra thì \(\Delta ABC\) phải thêm điều kiện cân tại \(A\).

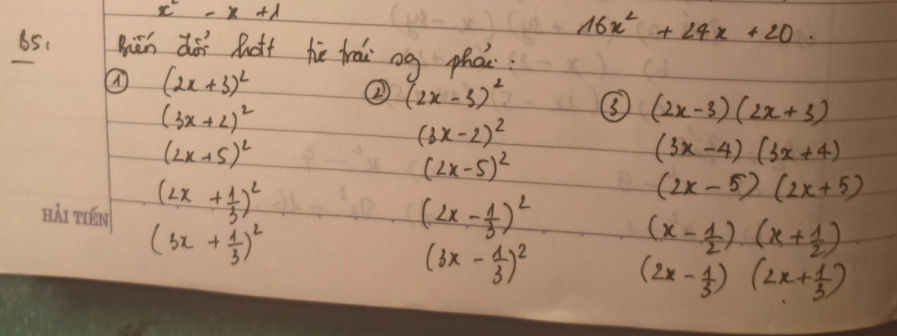

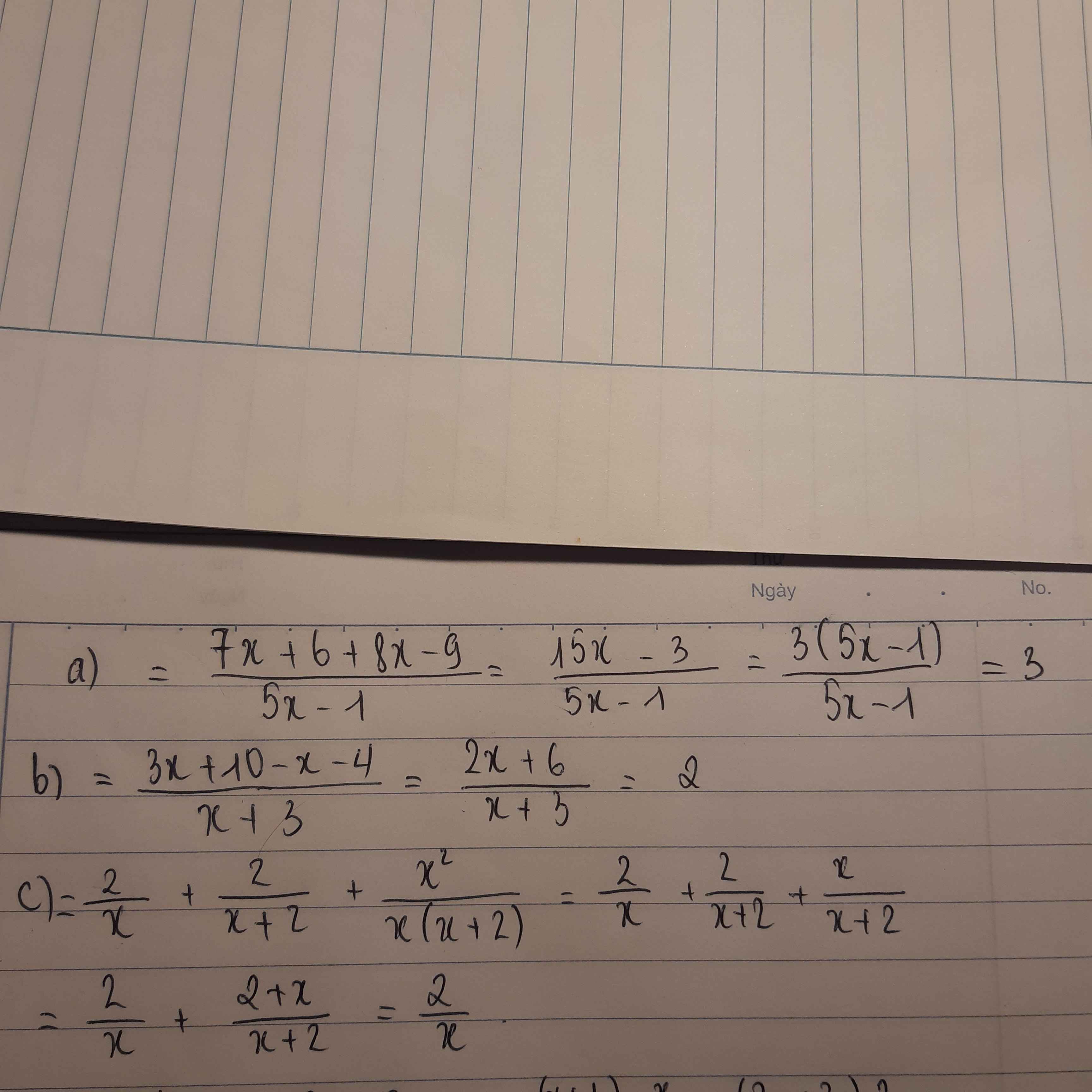


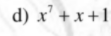



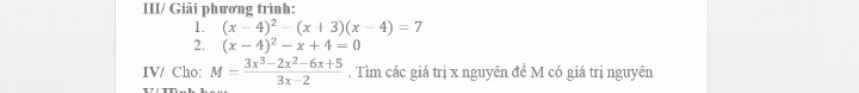

a: Xét ΔABC có
P là trung điểm của BC
N là trung điểm của AC
Do đó: PN là đường trung bình
=>PN//AM và PN=AM
=>AMPN là hình bình hành
mà AM=AN
nên AMPN là hình thoi
b: Xét ΔAPB vuông tại P có
\(AB^2=AP^2+BP^2\)
=>BP=4(cm)
=>BC=8(cm)
=>MN=4(cm)
\(S_{AMPN}=\dfrac{MN\cdot AP}{2}=\dfrac{4\cdot3}{2}=6\left(cm^2\right)\)