
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

\(=\left(3ay-15by\right)+\left(ax-5bx\right)=3y\left(a-5b\right)+x\left(a-5b\right)=\left(3y+x\right)\left(a-5b\right)\)

ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{2}{x-2}+\dfrac{3}{x+2}+\dfrac{18-5x}{4-x^2}=\dfrac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4+3x-6+5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10x-20}{\left(x-2\right)\left(x+2\right)}=\dfrac{10\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10}{x+2}\)

a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
góc N chung
=>ΔKNM đồng dạng với ΔMNP
b: \(MP=\sqrt{PK\cdot PN}=10\left(cm\right)\)

Bài 5:
a: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
b: =>5/3x-2/3+x=1+5/2-3/2x
=>25/6x=25/6
=>x=1
c: 3x-2=2x-3
=>3x-2x=-3+2
=>x=-1
d: =>2u+27=4u+27
=>u=0
e: =>5-x+6=12-8x
=>-x+11=12-8x
=>7x=1
=>x=1/7
f: =>-90+12x=-45+6x
=>12x-90=6x-45
=>6x-45=0
=>x=9/2

\(\left(3-2x\right)^2=\left(x-2\right)\left(2x-3\right)\)
\(\Leftrightarrow\left(3x-2\right)^2-\left(x-2\right)\left(2x-3\right)=0\)
\(\Leftrightarrow9x^2-12x+4-\left(2x^2-7x+6\right)=0\)
\(\Leftrightarrow9x^2-12x+4-2x^2+7x-6=0\)
\(\Leftrightarrow7x^2-5x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{2}{7}\end{matrix}\right.\)
Vậy \(S=\left\{1;-\dfrac{2}{7}\right\}\)
`(3-2x)^2=(x-2)(2x-3)`
`<=>(2x-3)^2 -(x-2)(2x-3)=0`
`<=> (2x-3)(2x-3-x+2)=0`
`<=> (2x-3)(x-1)=0`
\(< =>\left[{}\begin{matrix}2x-3=0\\x-1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=1\end{matrix}\right.\)

a: Xét tứ giác AECF có
AE//CF(AB//CD)
AE=CF
Do đó: AECF là hình bình hành
b: AE+EB=AB
CF+FD=CD
mà AE=CF và AB=CD
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE=BF
c:
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔAIC có
D,O lần lượt là trung điểm của AI,AC
=>DO là đường trung bình
=>DO//CI
d: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của EF
=>AC,EF,BD đồng quy(do cùng đi qua O)

1.\(ĐK:x\ne\pm2\)
\(\Leftrightarrow\dfrac{x+2}{x-2}-\dfrac{x-2}{x+2}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{\left(x+2\right)\left(x+2\right)-\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow\left(x+2\right)^2-\left(x-2\right)^2=4\)
\(\Leftrightarrow x^2+4x+4-x^2+4x-4=4\)
\(\Leftrightarrow8x=4\)
\(\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy S = \(\dfrac{1}{2}\)
2.\(ĐK:x\ne1;-3\)
\(\Leftrightarrow\dfrac{x+1}{x-1}-\dfrac{x+2}{x+3}=-\dfrac{4}{\left(x-1\right)\left(x+3\right)}\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+3\right)-\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}=-\dfrac{4}{\left(x-1\right)\left(x+3\right)}\)
\(\Rightarrow x^2+3x+x+3-x^2+x-2x+2=-4\)
\(\Leftrightarrow3x=-9\)
\(\Leftrightarrow x=-3\left(ktm\right)\)
Vậy S vô nghiệm
1) ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{x+2}{x-2}-\dfrac{x-2}{x+2}=\dfrac{4}{x^2-4}\)
\(\Leftrightarrow\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow x^2+4x+4-x^2+4x-4=4\)
\(\Leftrightarrow8x=4\)
\(\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy ....
2) ĐKXĐ:\(x\ne1,-3\)
\(\dfrac{x+1}{x-1}-\dfrac{x+2}{x+3}+\dfrac{4}{x^2+2x-3}=0\)
\(\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}-\dfrac{\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}+\dfrac{4}{x^2-x+3x-3}=0\)
\(\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}-\dfrac{\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}+\dfrac{4}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Rightarrow x^2+4x+3-x^2-x+2+4=0\)
\(\Leftrightarrow3x=-9\)
\(\Leftrightarrow x=-3\)(ktm)


 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
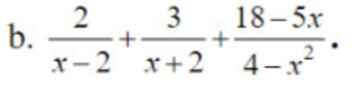 Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn
Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn

 Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Lời giải:
a.
$=(5x^2+5xy)+(10x+10y)=5x(x+y)+10(x+y)$
$=(x+y)(5x+10)=5(x+y)(x+2)$
b. Biểu thức không phân tích được thành nhân tử.