
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

Lời giải:
a.
$=(5x^2+5xy)+(10x+10y)=5x(x+y)+10(x+y)$
$=(x+y)(5x+10)=5(x+y)(x+2)$
b. Biểu thức không phân tích được thành nhân tử.

2
a) \(=x\left(3x^3-x^2+5\right)\)
b) \(=\left(2x+3y\right)\left(x-y\right)\)
c) \(=\left(x^2-3x\right)-\left(4x-12\right)=x\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x-4\right)\)
a, = x.(3x3 - x2 + 5)
b, = 2x.(x - y) + 3y.(x - y) = (x - y).(2x + 3y)
c, = x2 - 3x - 4x + 12 = (x2 - 3x) - (4x - 12) = x.(x - 3) - 4.(x - 3) = (x - 3).(x - 4)

\(=\left(3ay-15by\right)+\left(ax-5bx\right)=3y\left(a-5b\right)+x\left(a-5b\right)=\left(3y+x\right)\left(a-5b\right)\)

ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{2}{x-2}+\dfrac{3}{x+2}+\dfrac{18-5x}{4-x^2}=\dfrac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4+3x-6+5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10x-20}{\left(x-2\right)\left(x+2\right)}=\dfrac{10\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10}{x+2}\)

a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
góc N chung
=>ΔKNM đồng dạng với ΔMNP
b: \(MP=\sqrt{PK\cdot PN}=10\left(cm\right)\)

\(\dfrac{x+2}{x-3}< 0\)vì \(x+2>x-3\)
\(\left\{{}\begin{matrix}x+2>0\\x-3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x< 3\end{matrix}\right.\)<=> -2 < x < 3



 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
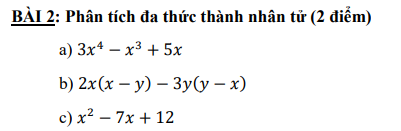

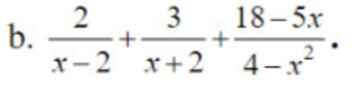 Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn
Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn

1.\(ĐK:x\ne\pm2\)
\(\Leftrightarrow\dfrac{x+2}{x-2}-\dfrac{x-2}{x+2}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{\left(x+2\right)\left(x+2\right)-\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow\left(x+2\right)^2-\left(x-2\right)^2=4\)
\(\Leftrightarrow x^2+4x+4-x^2+4x-4=4\)
\(\Leftrightarrow8x=4\)
\(\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy S = \(\dfrac{1}{2}\)
2.\(ĐK:x\ne1;-3\)
\(\Leftrightarrow\dfrac{x+1}{x-1}-\dfrac{x+2}{x+3}=-\dfrac{4}{\left(x-1\right)\left(x+3\right)}\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+3\right)-\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}=-\dfrac{4}{\left(x-1\right)\left(x+3\right)}\)
\(\Rightarrow x^2+3x+x+3-x^2+x-2x+2=-4\)
\(\Leftrightarrow3x=-9\)
\(\Leftrightarrow x=-3\left(ktm\right)\)
Vậy S vô nghiệm
1) ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{x+2}{x-2}-\dfrac{x-2}{x+2}=\dfrac{4}{x^2-4}\)
\(\Leftrightarrow\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow x^2+4x+4-x^2+4x-4=4\)
\(\Leftrightarrow8x=4\)
\(\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy ....
2) ĐKXĐ:\(x\ne1,-3\)
\(\dfrac{x+1}{x-1}-\dfrac{x+2}{x+3}+\dfrac{4}{x^2+2x-3}=0\)
\(\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}-\dfrac{\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}+\dfrac{4}{x^2-x+3x-3}=0\)
\(\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}-\dfrac{\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}+\dfrac{4}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Rightarrow x^2+4x+3-x^2-x+2+4=0\)
\(\Leftrightarrow3x=-9\)
\(\Leftrightarrow x=-3\)(ktm)