
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(x=\frac{10^{2015}\cdot7^{2016}}{2^{2015}\cdot35^{2016}}=\frac{2^{2015}\cdot5^{2015}\cdot7^{2016}}{2^{2015}\cdot5^{2016}\cdot7^{2016}}=\frac{1}{5}\)
b, \(x+2\)có ngoặc không vậy?
Nếu có: \(\frac{5^{x+2}}{25}=125\Rightarrow5^{x+2}=125\cdot25=3125=5^5\Rightarrow x+2=5\Rightarrow x=3\)
c, \(\left(\frac{3}{5}\right)^4\cdot\left(\frac{5}{3}\right)^3=\left(\frac{3}{5}\right)^3\cdot\left(\frac{5}{3}\right)^3\cdot\frac{3}{5}=\left(\frac{3}{5}\cdot\frac{5}{3}\right)^3\cdot\frac{3}{5}=1^3\cdot\frac{3}{5}=\frac{3}{5}\)
d, \(2\cdot x+7\)có ngoặc không vậy?
Nếu có: \(19\cdot5^{2\cdot x+7}=475\Rightarrow5^{2\cdot x+7}=\frac{475}{19}=25=5^2\Rightarrow2\cdot x+7=2\Rightarrow2\cdot x=-5\Rightarrow x=-\frac{5}{2}\)
e, Áp dụng tính chất dãy tỉ số bằng nhau
\(\Rightarrow\frac{x+2}{7}=\frac{y-3}{5}=\frac{z}{3}=\frac{x+2+y-3-z}{7+5-3}=\frac{-17-1}{9}=\frac{-18}{9}=2\)
\(\Rightarrow x+2=2\cdot7=14\Rightarrow x=12,y-3=2\cdot5=10\Rightarrow y=13,z=2\cdot3=6\)


Bài 4:
a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD


Ta có:
\(\frac{5}{1\cdot7}+\frac{5}{7\cdot13}+\frac{5}{13\cdot19}+...+\frac{5}{91\cdot97}\)
= \(5\cdot\frac{1}{6}\cdot\left(\frac{6}{1\cdot7}+\frac{6}{7\cdot13}+\frac{6}{13\cdot19}+...+\frac{6}{91\cdot97}\right)\)
= \(\frac{5}{6}\cdot\left(1-\frac{1}{7}+\frac{1}{7}-\frac{1}{13}+\frac{1}{13}-\frac{1}{19}+...+\frac{1}{91}-\frac{1}{97}\right)\)
= \(\frac{5}{6}\cdot\left(1-\frac{1}{97}\right)\)
= \(\frac{5}{6}\cdot\frac{96}{97}\)
= \(\frac{80}{97}\)
5/1.7 + 5/7.13 + 5/13.19 + ... + 5/91.97
= 5/6.(1 - 1/7 + 1/7 - 1/13 + 1/13 - 1/19 + ... + 1/91 - 1/97)
= 5/6.(1 - 1/97)
= 5/6.96/97
= 80/97

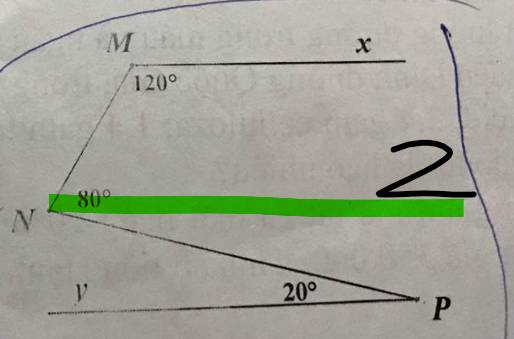
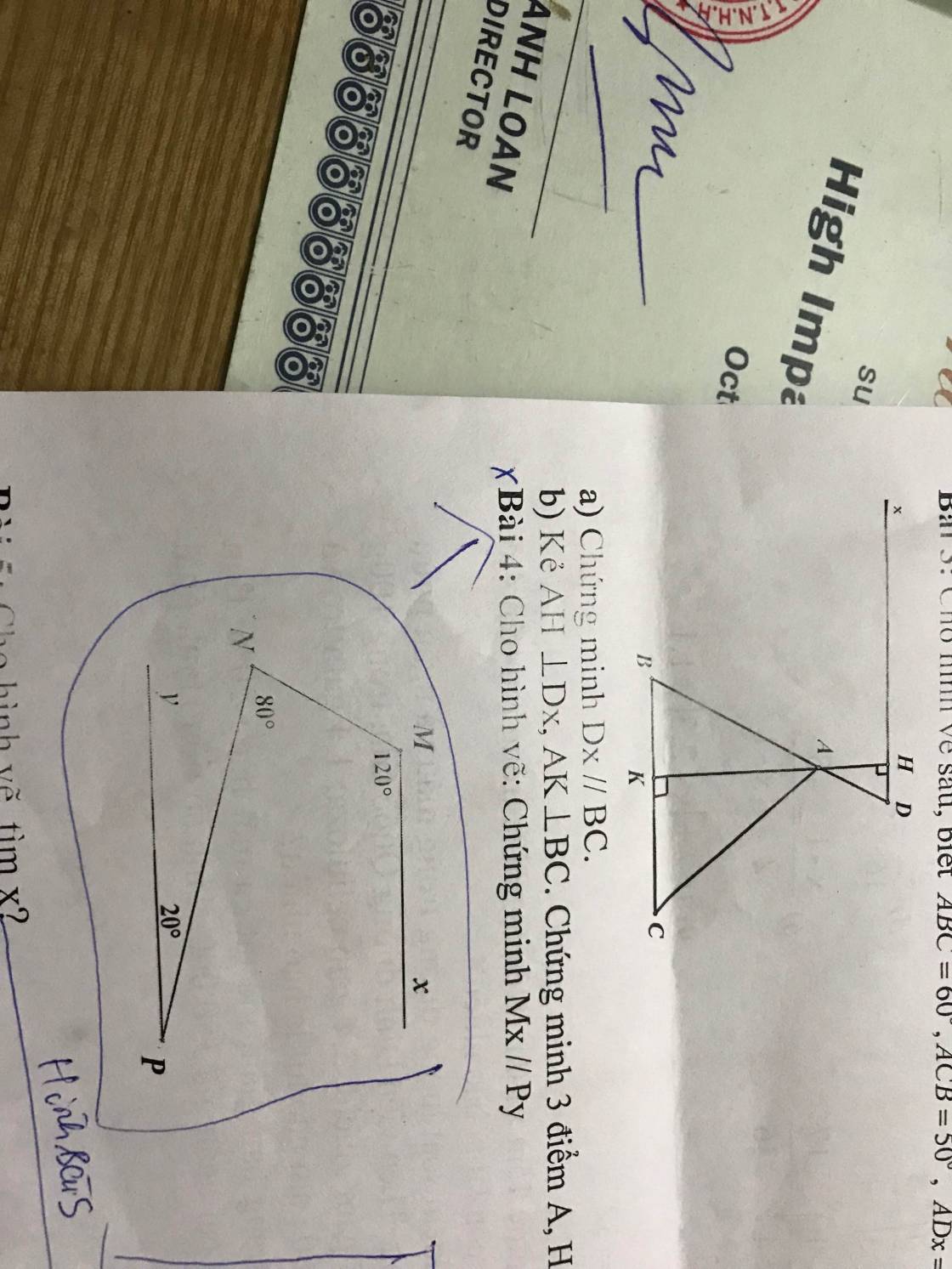
Qua N, kẻ tia Nz//Mx
Nz//Mx
=>\(\widehat{zNM}+\widehat{M}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{zNM}=60^0\)
\(\widehat{zNM}+\widehat{zNP}=\widehat{MNP}\)
=>\(\widehat{zNP}=80^0-60^0=20^0\)
\(\widehat{zNP}=\widehat{P}\)
mà hai góc này ở vị trí so le trong
nên Nz//Py
=>Mx//Py








\(\frac{2x+1}{5}=\frac{3y-2}{7}=\frac{2x+1+3y-2}{5+7}=\frac{2x+3y-1}{12}=\frac{2x+3y-1}{6x}.\)
\(\Rightarrow6x=12\Rightarrow x=2\)
\(\Rightarrow\frac{3y-2}{7}=\frac{2.2+1}{5}=1\Rightarrow y=3\)