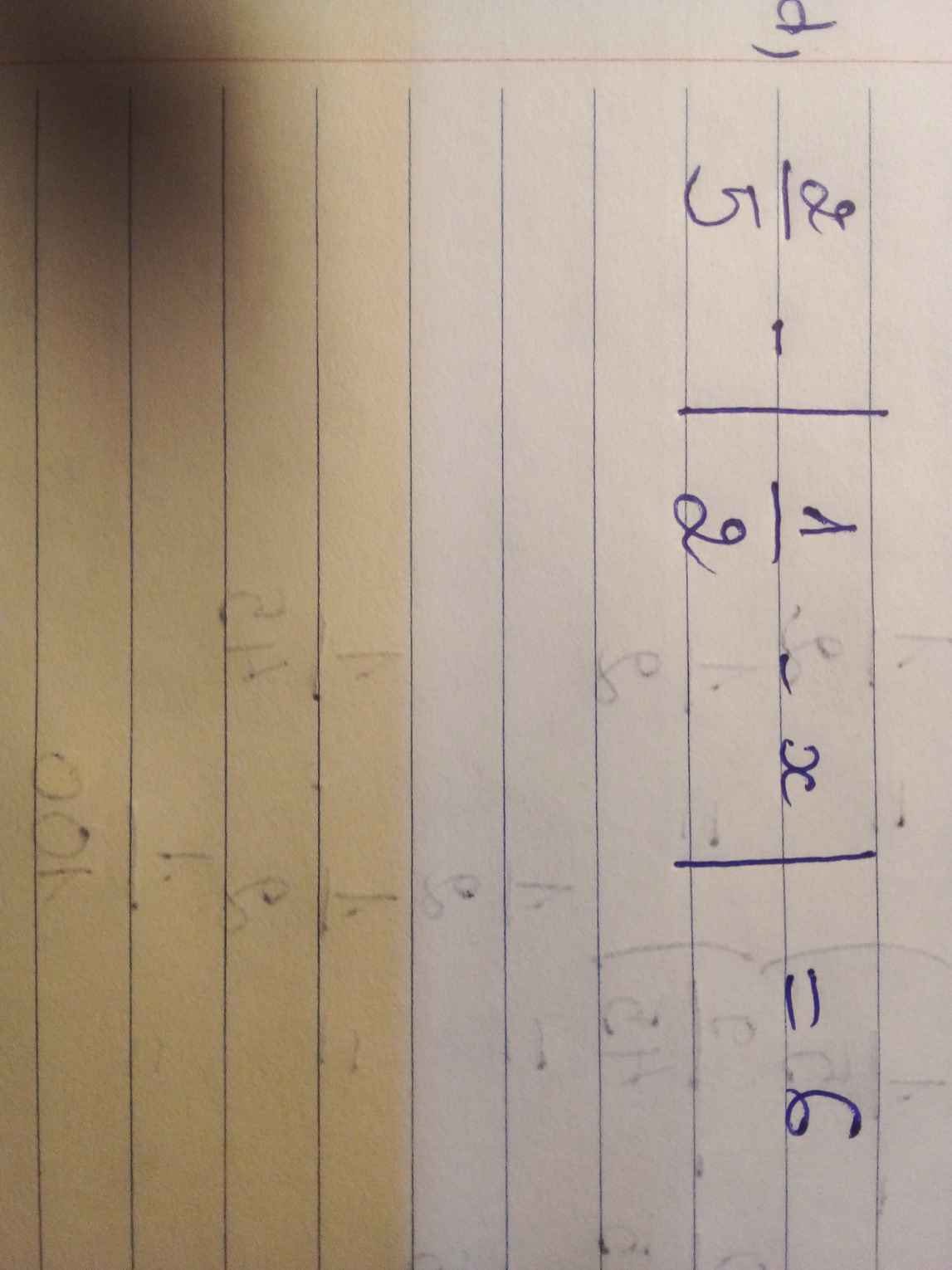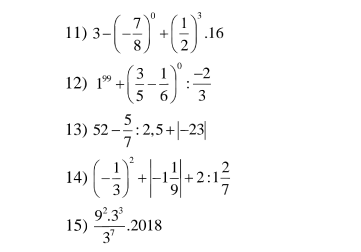K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HM
2
15 tháng 9 2021
\(\dfrac{2}{5}-\left|\dfrac{1}{2}-x\right|=6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=\dfrac{2}{5}-6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=-\dfrac{28}{5}\)( vô lý do \(\left|\dfrac{1}{2}-x\right|\ge0\forall x\))
Vậy \(x\in\left\{\varnothing\right\}\)
15 tháng 9 2021
\(\Rightarrow\left|\dfrac{1}{2}-x\right|=\dfrac{2}{5}-6=-\dfrac{28}{5}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}-x=-\dfrac{28}{5},\forall\dfrac{1}{2}-x\ge0\\\dfrac{1}{2}-x=\dfrac{28}{5},\forall\dfrac{1}{2}-x< 0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{61}{10},\forall x\le\dfrac{1}{2}\left(loại\right)\\x=-\dfrac{51}{10},\forall x>\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\Rightarrow x\in\varnothing\)
HT
3
H
11 tháng 4 2018
\(A=x^2+3x+3=x^2+2\cdot\frac{3}{2}\cdot x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+3\)
=> \(A=\left(x+\frac{3}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x+\frac{3}{2}\right)^2\ge0\) => \(A=\left(x+\frac{3}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)
=> Đa thức A vô nghiệm.
31 tháng 3 2016
Xét tam giác ABD và tam giác ACDcó AB+BD>AD vàAC+CD>AD(BĐT tam giác ABD và ACD)
Cộng 2 vế lại với nhau ta được:
AB+AC+BD+CD>2AD
=>AB+AC+BC>2AD
Mà AB+AC+BC là chu vi của tam giác ABC
=>1/2(AB+AC+BC)>AD
Vậy nửa chu vi của tam giác ABC>AD
16 tháng 10 2016
Ta có :
\(0,0\left(8\right)=\frac{4}{45}\)
\(0,1\left(2\right)=\frac{11}{90}\)
\(0,1\left(23\right)=\frac{61}{495}\)
16 tháng 10 2016
Ta có:
\(0,0\left(8\right)=0,0\left(1\right).8=\frac{0,\left(1\right)}{10}.8=\frac{1}{90}.8=\frac{8}{90}\)
Tương tự hết!
12 tháng 9 2016
0,0(8) = \(\frac{1}{10}\).0,(8) = \(\frac{1}{10}.\frac{8}{9}=\frac{4}{45}\)
31 tháng 10 2021
14: \(=\dfrac{1}{9}+\dfrac{10}{9}+2:\dfrac{9}{7}=\dfrac{11}{9}+\dfrac{14}{9}=\dfrac{25}{9}\)
15: \(=\dfrac{3^4\cdot3^3}{3^7}\cdot2018=2018\)
8 tháng 1 2022
a: Xét ΔOMA và ΔOMB có
OM chung
MA=MB
OA=OB
Do đó: ΔOMA=ΔOMB
Suy ra: \(\widehat{AOM}=\widehat{BOM}\)
hay OM là tia phân giác của góc xOy
b: Xét tứ giác OMAP có
N là trung điểm của OA
N là trung điểm của MP
Do đó: OMAP là hình bình hành
Suy ra: OP=AM và OP//AM
H
17 tháng 11 2021
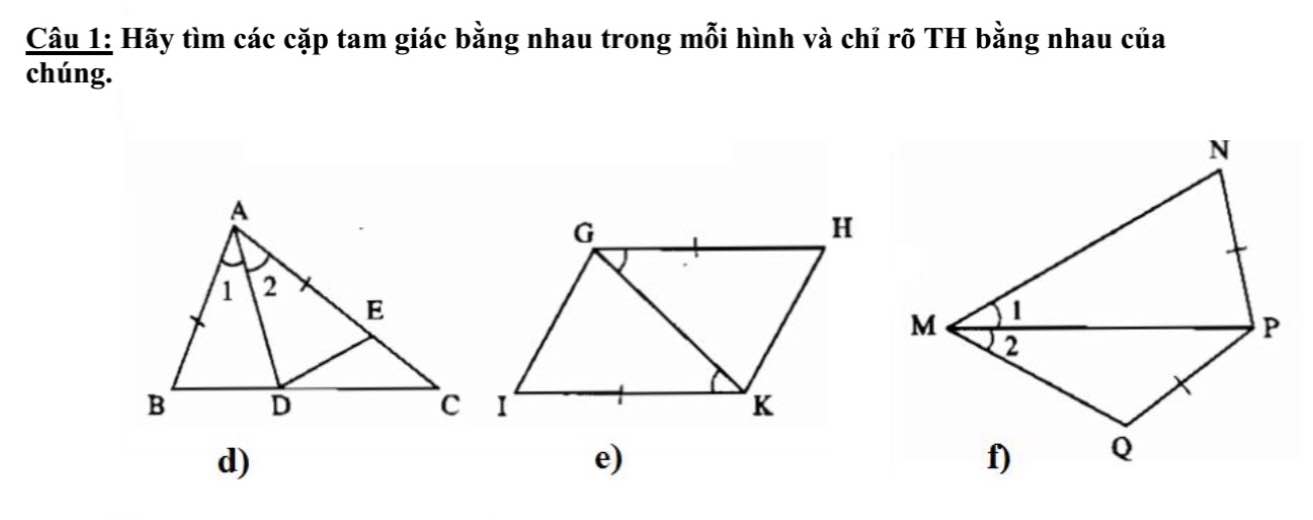
a, Tam giác ABD và tam giác AED ( c-g-c)
b, Tam giác GKI và tam giác HGK ( c-g-c)
c,tam giác QMP và tam giác NMP ( c-g-c)
17 tháng 11 2021
d)△ABD=△AED (c.g.c)
e)△GIK=△KHG (c.g.c)
f)Ko có tam giác bằng nhau vì không có góc xen giữa 2 cạnh bằng nhau