K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 1 2022
a:Thay x=49 vào A, ta được:
\(A=\dfrac{2\cdot7-10}{7-3}=\dfrac{4}{4}=1\)
b: \(B=\dfrac{3\sqrt{x}-15+20-2\sqrt{x}}{x-25}=\dfrac{1}{\sqrt{x}-5}\)
QN
0
PC
1
LA
1
31 tháng 7 2021
b) Để P nguyên thì \(\sqrt{x}+5⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}+15⋮3\sqrt{x}-1\)
\(\Leftrightarrow16⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}-1\in\left\{-1;1;2;4;8;16\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;2;3;5;9;17\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
hay \(x\in\left\{0;1;9\right\}\)
16 tháng 8 2021
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AK là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AFKE có
\(\widehat{AFK}=\widehat{AEK}=\widehat{EAF}=90^0\)
Do đó: AFKE là hình chữ nhật
Suy ra: \(AK=FE\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(AE\cdot AB=FE^2\)
c: Ta có: \(AF\cdot AC+AE\cdot AB+KB\cdot KC\)
\(=AK^2+AK^2+AK^2\)
\(=3\cdot AK^2=3\cdot FE^2\)
N
20 tháng 11 2021
\(a,C=\dfrac{81-1}{4\cdot9}=\dfrac{80}{36}=\dfrac{20}{9}\\ b,D=\dfrac{x+2\sqrt{x}+1+x-\sqrt{x}+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ D=\dfrac{2x+2\sqrt{x}+1}{x-1}\\ c,CD=\dfrac{x-1}{4\sqrt{x}}\cdot\dfrac{2x+2\sqrt{x}+1}{x-1}=\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{13}{8}\\ \Leftrightarrow52\sqrt{x}=16x+16\sqrt{x}+8\\ \Leftrightarrow16x-36\sqrt{x}+8=0\\ \Leftrightarrow4x-9\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{1}{16}\left(tm\right)\end{matrix}\right.\)
\(d,N=CD=\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{\sqrt{x}}{2}+\dfrac{1}{2}+\dfrac{1}{4\sqrt{x}}\\ \Leftrightarrow N\ge2\sqrt{\dfrac{\sqrt{x}}{2}\cdot\dfrac{1}{4\sqrt{x}}}+\dfrac{1}{2}=2\sqrt{\dfrac{1}{8}}+\dfrac{1}{2}=\dfrac{\sqrt{2}+1}{2}\)
Dấu \("="\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy \(N_{min}=\dfrac{\sqrt{2}+1}{2}\)
22 tháng 8 2021
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có KA là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AEKF có
\(\widehat{FAE}=\widehat{AFK}=\widehat{AEK}=90^0\)
Do đó: AEKF là hình chữ nhật
Suy ra: \(AK=EF\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(EF^2=AE\cdot AB\)
c: Ta có: \(AE\cdot AB+AF\cdot AC+KB\cdot KC\)
\(=AH^2+AH^2+AH^2\)
\(=3\cdot EF^2\)
T
1
2 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
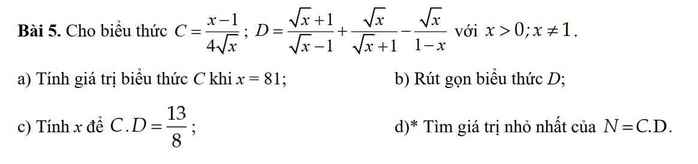
k đùa