
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1, Đề thiếu rồi bạn
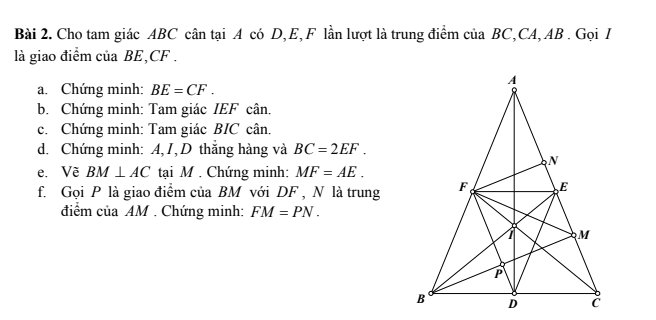
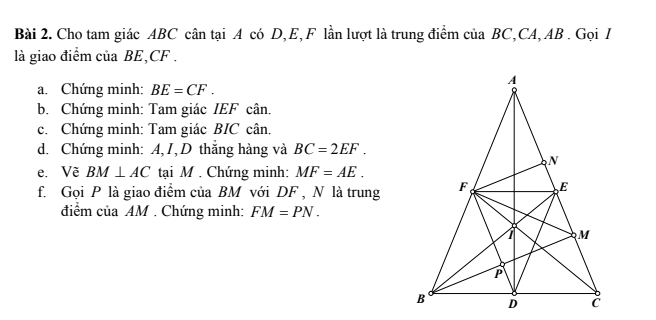
2, Gọi tam giác ABC
Áp dụng t/c dtsbn:
\(\dfrac{AB}{2}=\dfrac{BC}{3}=\dfrac{CA}{4}=\dfrac{AB+BC+CA}{2+3+4}=\dfrac{45}{9}=5\\ \Rightarrow\left\{{}\begin{matrix}AB=10\left(cm\right)\\BC=15\left(cm\right)\\CA=20\left(cm\right)\end{matrix}\right.\)
Vậy 3 cạnh của tam giác lần lượt là 10cm,15cm,20cm




\(B=2022^0+\left(-1\right)^{2021}+\left(-\dfrac{3}{2}\right)^2:\sqrt{\dfrac{9}{4}}-\left|-\dfrac{2}{3}\right|\)
\(=1-1+\dfrac{9}{4}:\dfrac{3}{2}-\dfrac{2}{3}\)
\(=\dfrac{9}{4}\cdot\dfrac{2}{3}-\dfrac{2}{3}\)
\(=\dfrac{3}{2}-\dfrac{2}{3}\)
\(=\dfrac{5}{6}\)

a) Do \(\left(3x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\)
\(minA=-4\Leftrightarrow x=\dfrac{1}{6}\)
b) Do \(\left(2x+1\right)^4\ge0\forall x,\left(y-\dfrac{1}{2}\right)^6\ge0\forall y\)
\(\Rightarrow B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\)
\(minB=0\Leftrightarrow\)\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
a: \(A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{6}\)
b: \(B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\)


\(\left(x-3\right)^{30}=\left(x-3\right)^{10}\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=4\end{matrix}\right.\)


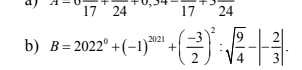
 giúp mình 2 câu này với ạ mình đang cần gấp
giúp mình 2 câu này với ạ mình đang cần gấp
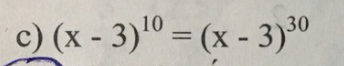 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp
1: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB
Bạn giải giúp mình phần 2 đk mình đang cần phần 2