
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB

\(\left(x-3\right)^{30}=\left(x-3\right)^{10}\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=4\end{matrix}\right.\)

b: Ta có: \(\left(\dfrac{3}{5}-\dfrac{2}{3}x\right)^3=\dfrac{-64}{125}\)
\(\Leftrightarrow\dfrac{3}{5}-\dfrac{2}{3}x=\dfrac{-4}{5}\)
\(\Leftrightarrow x\cdot\dfrac{2}{3}=\dfrac{3}{5}+\dfrac{4}{5}=\dfrac{7}{5}\)
hay \(x=\dfrac{7}{5}:\dfrac{2}{3}=\dfrac{21}{10}\)



a) Do \(\left(3x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\)
\(minA=-4\Leftrightarrow x=\dfrac{1}{6}\)
b) Do \(\left(2x+1\right)^4\ge0\forall x,\left(y-\dfrac{1}{2}\right)^6\ge0\forall y\)
\(\Rightarrow B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\)
\(minB=0\Leftrightarrow\)\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
a: \(A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{6}\)
b: \(B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\)


`@` `\text {Ans}`
`\downarrow`
`c)`
\(2-3^{x-1}-7=11\)
`\Rightarrow`\(3^{x-1}-5=11\)
`\Rightarrow`\(3^{x-1}=11+5\)
`\Rightarrow`\(3^{x-1}=16\)
Bạn xem lại đề
`d)`
\(\left(x-\dfrac{3}{5}\right)\div\dfrac{-1}{3}=-0,4\)
`\Rightarrow`\(x-\dfrac{3}{5}=-0,4\cdot\left(-\dfrac{1}{3}\right)\)
`\Rightarrow`\(x-\dfrac{3}{5}=\dfrac{2}{15}\)
`\Rightarrow`\(x=\dfrac{2}{15}+\dfrac{3}{5}\)
`\Rightarrow`\(x=\dfrac{11}{15}\)
Vậy, \(x=\dfrac{11}{15}\)

Bài kiểm tra tôt snhaats dựa vào câu trl khác đi, lớp 5 ko rõ bằng lớp 7 đâu!


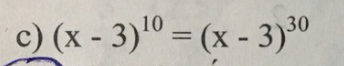 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp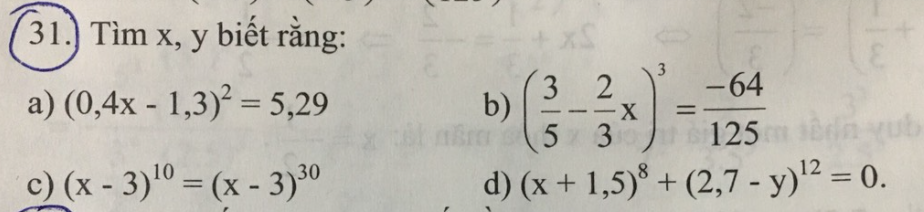 giúp mình 4 câu này với mình đang cần gấp
giúp mình 4 câu này với mình đang cần gấp 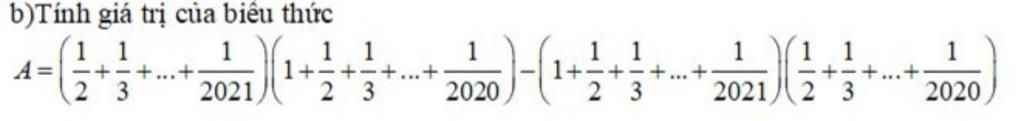
 giúp mình 2 câu này với ạ mình đang cần gấp
giúp mình 2 câu này với ạ mình đang cần gấp

 câu c với , mình đang cần gấp
câu c với , mình đang cần gấp em mới lớp 5 sai thì bỏ qua nhé!
em mới lớp 5 sai thì bỏ qua nhé!
1, Đề thiếu rồi bạn
2, Gọi tam giác ABC
Áp dụng t/c dtsbn:
\(\dfrac{AB}{2}=\dfrac{BC}{3}=\dfrac{CA}{4}=\dfrac{AB+BC+CA}{2+3+4}=\dfrac{45}{9}=5\\ \Rightarrow\left\{{}\begin{matrix}AB=10\left(cm\right)\\BC=15\left(cm\right)\\CA=20\left(cm\right)\end{matrix}\right.\)
Vậy 3 cạnh của tam giác lần lượt là 10cm,15cm,20cm
câu 1 ko thiếu đâu bạn, đúng rồi đấy