
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b: Vì (d)//y=-2x+5/2 nên a=-2
Vậy: y=-2x+b
Phương trình hoành độ giao điểm là:
\(0.5x^2+2x-b=0\)
\(\Delta=2^2-4\cdot0.5\cdot\left(-b\right)=4+2b\)
Để (d) tiếp xúc với (P) thì 2b+4=0
hay b=-2

Gọi số kg vật liệu xưởng phải sản xuất mỗi ngày theo kế hoạch là \(x\left(kg\right)\left(0< x< 216\right)\)
Thời gian dự định sản xuất là \(\dfrac{216}{x}\) (ngày)
Ba ngày đầu tiên khối lượng vật liệu sản xuất được là \(3x\left(kg\right)\)
Số vật liệu còn lại là \(232-3x\)
Thời gian sản xuất số vật liệu còn lại là \(\dfrac{232-3x}{x+8}\)
Ta có phương trình:
\(\dfrac{216}{x}=3+\dfrac{232-3x}{x+8}+1\)
\(\Rightarrow216\left(x+8\right)=4x\left(x+8\right)+\left(232-3x\right)x\)
\(\Rightarrow216x+1728=4x^2+32x+232x-3x^2\)
\(\Rightarrow x^2+48x-1728=0\Rightarrow\left[{}\begin{matrix}x=24\left(TM\right)\\x=-72\left(L\right)\end{matrix}\right.\)
Vậy theo kế hoạch mỗi ngày xưởng phải sản xuất 24 kg vật liệu.


`#Hưng`
\(a,3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\\ =\sqrt{9.8\sqrt{5}}-\sqrt{4.9\sqrt{20}}\\ =\sqrt{72\sqrt{5}}-\sqrt{36\sqrt{20}}\\ =\sqrt{\sqrt{5184.5}}-\sqrt{\sqrt{1296.20}}\\ =\sqrt{\sqrt{25920}}-\sqrt{\sqrt{25920}}\\ =0\)
\(b,ĐKXĐ:x\sqrt{x}-\sqrt{x}+x-1\ne0\\ \Rightarrow\sqrt{x}\left(x-1\right)+\left(x-1\right)\ne0\\ \Rightarrow\left(x-1\right)\left(\sqrt{x}+1\right)\ne0\\ \Rightarrow x-1\ne0\left(vì.\sqrt{x}+1>0\right)\\ \Rightarrow x\ne1\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)
\(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{1-\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\)
Khi \(x=\left(2-\sqrt{3}\right)^2\) thì
\(P=\dfrac{2}{\left(2-\sqrt{3}\right)^2+\sqrt{\left(2-\sqrt{3}\right)^2}+1}\)
\(P=\dfrac{2}{7-4\sqrt{3}+2-\sqrt{3}+1}\)
\(=\dfrac{2}{10-5\sqrt{3}}=\dfrac{4+2\sqrt{3}}{5}\)
c: P>=2/3
=>P-2/3>=0
=>\(\dfrac{2}{x+\sqrt{x}+1}-\dfrac{2}{3}>=0\)
=>\(\dfrac{1}{x+\sqrt{x}+1}-\dfrac{1}{3}>=0\)
=>\(\dfrac{3-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}>=0\)
=>\(-x-\sqrt{x}+2>=0\)
=>\(x+\sqrt{x}-2< =0\)
=>\(\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)< =0\)
=>\(\sqrt{x}-1< =0\)
=>0<=x<=1
Kết hợp ĐKXĐ, ta được: 0<=x<1

a) Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)


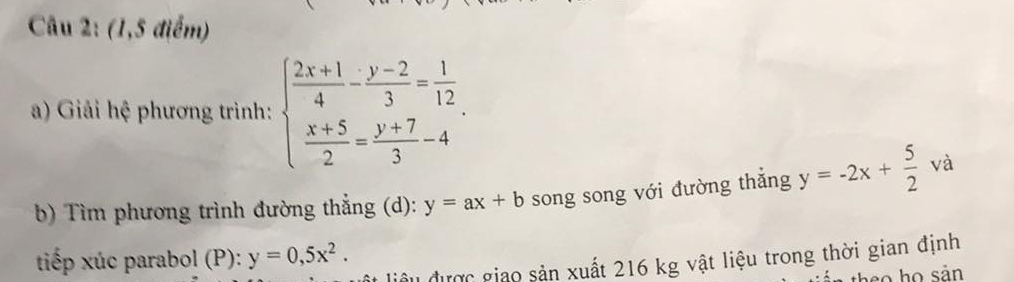


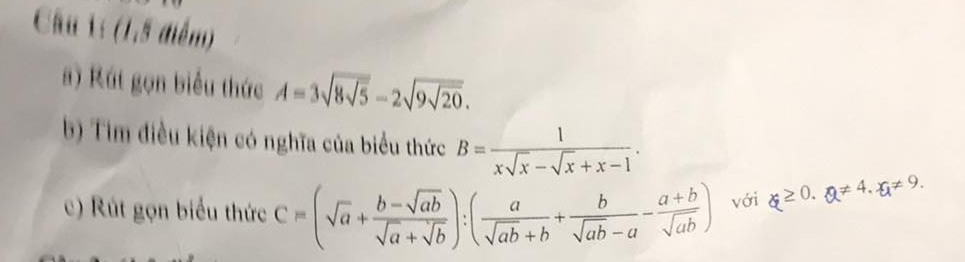


26D
27B
28C
29A
30B
31B
32C