
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b. \(\Delta=b^2-4ac=\left[-\left(3m-2\right)\right]^2-4\cdot1\cdot\left(-3m\right)=9m^2+4>0\forall m\)
=> phuong trình luôn có 2 nghiệm phân biệt.


\(g,ĐK:x\ge0\\ PT\Leftrightarrow10\sqrt{x}+8\sqrt{x}-11\sqrt{x}=21\\ \Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ h,ĐK:x\ge0\\ PT\Leftrightarrow6\sqrt{3x}+2\sqrt{3x}-3\sqrt{3x}=15\\ \Leftrightarrow\sqrt{3x}=5\Leftrightarrow3x=25\Leftrightarrow x=\dfrac{25}{3}\left(tm\right)\\ i,ĐK:x\ge0\\ PT\Leftrightarrow12\sqrt{x}-21-2\sqrt{x}+10=6\sqrt{x}-12\\ \Leftrightarrow4\sqrt{x}=-1\Leftrightarrow\sqrt{x}=-\dfrac{1}{4}\Leftrightarrow x\in\varnothing\\ j,ĐK:x\ge2\\ PT\Leftrightarrow6\sqrt{x-2}-15\cdot\dfrac{1}{5}\sqrt{x-2}=20+4\sqrt{x-2}\\ \Leftrightarrow\sqrt{x-2}=-20\Leftrightarrow x\in\varnothing\)
\(k,ĐK:x\ge3\\ PT\Leftrightarrow6\sqrt{x-3}-\dfrac{1}{5}\cdot5\sqrt{x-3}-\dfrac{1}{7}\cdot7\sqrt{x-3}=20\\ \Leftrightarrow4\sqrt{x-3}=20\Leftrightarrow\sqrt{x-3}=5\\ \Leftrightarrow x-3=25\Leftrightarrow x=28\left(tm\right)\\ l,ĐK:x\ge5\\ PT\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=4\\ \Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\\ \Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)

\(\left\{{}\begin{matrix}3x-2y=-2\\2x+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=-2\\4x+2y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=0\\2x+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2.0+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\0+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Vậy...
\(\left\{{}\begin{matrix}3x-2y=-2\\2x+y=1\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}3x-2y=-2\\4x+2y=2\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}7x=0\\2x+y=1\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x=0\\2.0+y=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
vậy...

a: \(P=\dfrac{\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{x-4}{4}=\dfrac{\sqrt{x}}{2}\)

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do dó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC(3)
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC⊥CD(4)
Từ (3) và (4) suy ra OA//CD






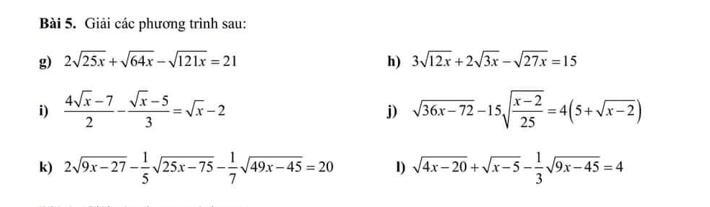
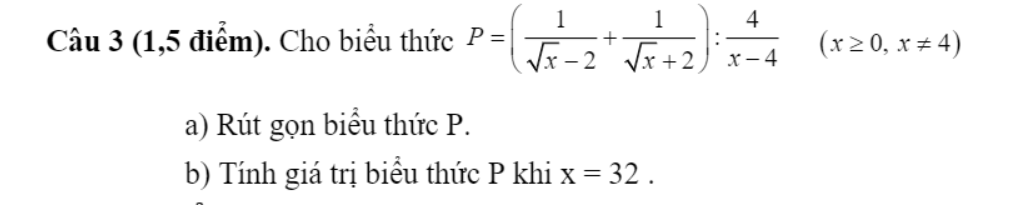

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)
\(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{1-\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\)
Khi \(x=\left(2-\sqrt{3}\right)^2\) thì
\(P=\dfrac{2}{\left(2-\sqrt{3}\right)^2+\sqrt{\left(2-\sqrt{3}\right)^2}+1}\)
\(P=\dfrac{2}{7-4\sqrt{3}+2-\sqrt{3}+1}\)
\(=\dfrac{2}{10-5\sqrt{3}}=\dfrac{4+2\sqrt{3}}{5}\)
c: P>=2/3
=>P-2/3>=0
=>\(\dfrac{2}{x+\sqrt{x}+1}-\dfrac{2}{3}>=0\)
=>\(\dfrac{1}{x+\sqrt{x}+1}-\dfrac{1}{3}>=0\)
=>\(\dfrac{3-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}>=0\)
=>\(-x-\sqrt{x}+2>=0\)
=>\(x+\sqrt{x}-2< =0\)
=>\(\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)< =0\)
=>\(\sqrt{x}-1< =0\)
=>0<=x<=1
Kết hợp ĐKXĐ, ta được: 0<=x<1