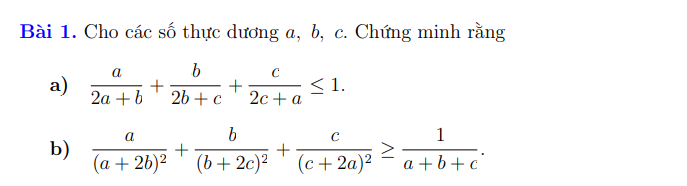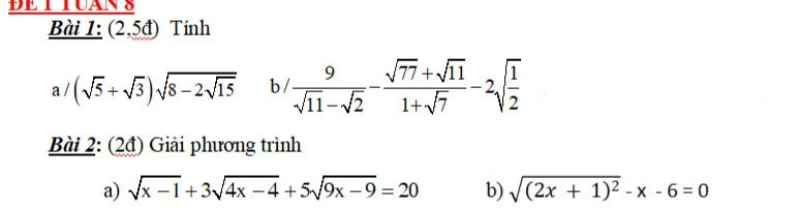K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 3 2021
a) Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
9 tháng 7 2021
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{C}+35^0=90^0\)
hay \(\widehat{C}=55^0\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan35^0\)
\(\Leftrightarrow AC=6\cdot\tan35^0\)
hay \(AC\simeq4,2\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+4.2^2=53.64\)
hay \(BC\simeq7.32\left(cm\right)\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot7.32=4.2\cdot6=25.2\)
hay \(AH\simeq3.44\left(cm\right)\)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\dfrac{1}{2}BC\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(AM=\dfrac{1}{2}\cdot7.32=3.66\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAHM vuông tại H, ta được:
\(AM^2=AH^2+MH^2\)
\(\Leftrightarrow MH^2=3.66^2-3.44^2=1.562\)
hay \(MH\simeq1.25\left(cm\right)\)
Diện tích tam giác AHM là:
\(S_{AHM}=\dfrac{AH\cdot HM}{2}=\dfrac{3.44\cdot1.25}{2}=2.15\left(cm^2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
a.
\(\Leftrightarrow\dfrac{2a}{2a+b}+\dfrac{2b}{2b+c}+\dfrac{2c}{2c+a}\le2\)
\(\Leftrightarrow\dfrac{2a}{2a+b}-1+\dfrac{2b}{2b+c}-1+\dfrac{2c}{2c+a}-1\le-1\)
\(\Leftrightarrow\dfrac{b}{2a+b}+\dfrac{c}{2b+c}+\dfrac{a}{2c+a}\ge1\)
Thật vậy, ta có:
\(VT=\dfrac{b^2}{2ab+b^2}+\dfrac{c^2}{2bc+c^2}+\dfrac{a^2}{2ca+a^2}\ge\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2+2ab+2bc+2ca}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
b.
Chuẩn hóa \(a+b+c=1\), BĐT cần chứng minh trở thành:
\(\dfrac{a}{\left(a+2b\right)^2}+\dfrac{b}{\left(b+2c\right)^2}+\dfrac{c}{\left(c+2a\right)^2}\ge1\)
Ta có:
\(\dfrac{a}{\left(a+2b\right)^2}+a\left(a+2b\right)+a\left(a+2b\right)\ge3a\)
Tương tự:
\(\dfrac{b}{\left(b+2c\right)^2}+b\left(b+2c\right)+b\left(b+2c\right)\ge3b\)
\(\dfrac{c}{\left(c+2a\right)^2}+c\left(c+2a\right)+c\left(c+2a\right)\ge3c\)
Cộng vế:
\(VT+2\left(a+b+c\right)^2\ge3\left(a+b+c\right)\)
\(\Leftrightarrow VT+2\ge3\)
\(\Leftrightarrow VT\ge1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
LB
1
25 tháng 8 2021
Câu 3:
2: Xét tứ giác OKEH có
\(\widehat{OKE}=\widehat{OHE}=\widehat{KOH}=90^0\)
Do đó: OKEH là hình chữ nhật
mà đường chéo OE là tia phân giác của \(\widehat{KOH}\)
nên OKEH là hình vuông
5 tháng 11 2021
Bài 1:
a: \(=\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)=2\)
b: \(=\sqrt{11}+\sqrt{2}-\sqrt{11}-\sqrt{7}-\sqrt{2}=-\sqrt{7}\)
TH
1
28 tháng 2 2022
Câu 1:
Gọi chiều rộng là x
Chiều dài là x+20
Theo đề, ta có: 2(x+x+20)=104
=>2x+20=52
=>2x=32
hay x=16
Vậy: Diện tích của miếng đất là 16x36=576(m2)
28 tháng 2 2022
Xin lỗi nhưng e cần bài này dạng Giải bài bằng cách lập hệ phương trình ạ
rút gọn biểu thức
7 tháng 2 2022
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{1}{\sqrt{x}+1}\left(đk:x\ne1,x\ge0\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-2\sqrt{x}-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}-2\sqrt{x}-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
AM
7 tháng 2 2022
ĐKXĐ: \(x\ne1,x\ge0\)
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{1}{\sqrt{x}+1}=\)\(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{\sqrt{x}-1}{x-1}=\)\(\dfrac{x+\sqrt{x}-2\sqrt{x}-\sqrt{x}+1}{x-1}=\)\(\dfrac{x-2\sqrt{x}+1}{x-1}=\)\(\dfrac{(\sqrt{x}-1)^2}{x-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)