
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



x^7+x^5+1=x^7+x^6+x^5-x^6+1
=x^5(x^2+x+1)-[(x^3)^2-1]
=x^5(x^2+x+1)-(x^3+1)(x^3-1)
=x^5(x^2+x+1)-(x^3+1)(x-1)(x^2+x+1)
=(x^2+x+1)[x^5-(x^3+1)(x-1)]
=(x^2+x+1)(x^5-x^4+x^3-x+1)

Trả lời:
\(M=\left(x-2020\right)^4+\left(x+y+1\right)^2+5\)
Ta có: \(\left(x-2020\right)^4\ge0\forall x;\left(x+y+1\right)^2\ge0\forall x,y\)
\(\Rightarrow\left(x-2020\right)^4+\left(x+y+1\right)^2\ge0\forall x,y\)
\(\Rightarrow\left(x-2020\right)^4+\left(x+y+1\right)^2+5\ge5\forall x,y\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x-2020=0\\x+y+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2020\\y=-2021\end{cases}}}\)
Vậy GTNN của M = 5 khi x = 2020; y = - 2021

`@` `\text {Ans}`
`\downarrow`
Ta có:
`A(x) = B(x)* Q(x) - x + 1`
`A(x) = x^3-2x^2+x`; `Q(x) = x - 1`
`<=> B(x) * (x - 1) - x + 1 = x^3 - 2x^2 + x`
`<=> B(x) * (x - 1) = x^3 - 2x^2 + x + x - 1`
`<=> B(x) * (x - 1) = x^3 - 2x^2 + 2x - 1`
`<=> B(x) = (x^3 - 2x^2 + 2x - 1) \div (x - 1)`
`<=> B(x) = x^2 - x + 1`
Vậy, `B(x) = x^2 - x + 1.`
A(x)=B(x)*Q(x)-x+1
=>x^3-2x^2+x=B(x)(x-1)-x+1
=>B(x)*(x-1)=x^3-2x^2+x+x-1=x^3-2x^2+2x-1
=>\(B\left(x\right)=\dfrac{x^3-2x^2+2x-1}{x-1}=\dfrac{\left(x-1\right)\left(x^2+x+1\right)-2x\left(x-1\right)}{x-1}\)
=>B(x)=x^2+x+1-2x
=>B(x)=x^2-x+1

ta có :
\(P\left(x^2\right)=x^2\left(x^2+1\right)P\left(x\right)\Rightarrow\frac{P\left(x^2\right)}{x^4\left(x^4-1\right)}=\frac{P\left(x\right)}{x^2\left(x^2-1\right)}\)
Đặt \(f\left(x\right)=\frac{P\left(x\right)}{x^2\left(x^2-1\right)}\Rightarrow f\left(x\right)=f\left(x^2\right)\forall x\Rightarrow f\left(x\right)=f\left(-x\right)=f\left(x^2\right)\)
\(\Rightarrow f\left(x\right)=f\left(\sqrt{x}\right)=...=f\left(\sqrt[2^n]{x}\right)=f\left(1\right)\) với mọi x>0
nên ta có f(x) là hàm hằng
hay \(\frac{P\left(x\right)}{x^2\left(x^2-1\right)}=c\text{ mà }P\left(2\right)=2\Rightarrow c=\frac{1}{6}\)
Vậy \(P\left(x\right)=\frac{1}{6}\left(x^2\left(x^2-1\right)\right)\)


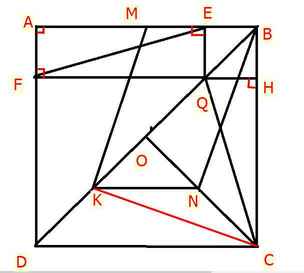
a) Ta có : \(\widehat{AEQ}=\widehat{EAF}=\widehat{AFQ}=90\)
➜ AEQF là hình chữ nhật ( DHNB hình chữ nhật )
b) Vì ABCD là hình vuông ➝ \(\widehat{ABD}=45\) ↔ \(\widehat{EBQ}=45\)
Mà ΔEBQ vuông tại E
➜ ΔEBQ vuông cân tại E
➝ EB = EQ
Mà \(\left\{{}\begin{matrix}FQ=AE\\AE+EB=AB\end{matrix}\right.\)
➞ QE + QF = AB
d) Ta có : AB = DC ( ABCD là hình vuông )
⇔ \(\dfrac{1}{2}DC=\dfrac{1}{2}AB=BM\)
Xét tam giác DOC có : K, N là trung điểm OD , OC
=> KN = \(\dfrac{1}{2}DC\) , KN // DC
Mà \(\dfrac{1}{2}DC=\dfrac{1}{2}AB=BM\) , DC // BM
=> KN = BM , KN // BM
=> KNBM là hình bình hành ( BDNB hình bình hành )
e) Ta có : KN ⊥ BC ( KN // AB // FH , FH ⊥ BC )
Lại có : AC ⊥ BD ( ABCD là hình vuông )
↔ CN ⊥ BD
Xét tam giác BCK có : CN ⊥ BD ; KN ⊥ BC
→ N là trực tâm Δ BCK
→ BN ⊥ KC
Mà BN // MK ( MBNK là hình bình hành )
→ MK ⊥ KC
➢ ĐPCM

1: ΔABC vuông tại A
=>góc BAC=90 độ
2: BE là phân giác của góc ABC
=>góc ABE=góc CBE
Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc CBE
Do đó: ΔABE=ΔHBE
3: ΔABE=ΔHBE
=>BA=BH và EA=EH
=>BE là trung trực của AH

2.
Gọi quãng đường AB là x(km) ( x>0 )
Thời gian đi là \(\dfrac{x}{20}\)
Thời gian về là \(\dfrac{x}{15}\)
Theo đề bài, ta có:
\(\dfrac{x}{15}-\dfrac{x}{20}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{4x-3x}{60}=\dfrac{10}{60}\)
\(\Leftrightarrow x=10\left(tm\right)\)
Vậy quãng đường AB dài 10km

 help pls
help pls

bằng2
1+1=2
#hỏi ngu thía!...:((