Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
? Lời giải:
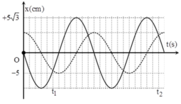
+ Đặt đường trên là dao động (1), đường dưới là dao động (2).
φ 1 = 2 π 3 → t = 0 , 9 α 1 = ω 1 t + φ 1 ⇔ 4 π 3 = ω 1 .0 , 9 + 2 π 3 ⇒ ω 1 = 20 π 27 r a d / s
+ Từ đồ thị ta nhận thây hai đường thẳng song song với nhau suy ra ω 2 = ω 1 .
+ Khi t = 0 , 3 s ⇒ α 2 = ω 2 t + φ 2 ⇔ − 2 π 3 = 20 π 7 .0 , 3 + φ 2 ⇒ φ 2 = − 8 π 9
⇒ x 1 = A cos 20 π 7 t + 2 π 3 x 2 = A cos 20 π 7 t − 8 π 9 ⇒ Δ x = x 1 − x 2 = C ⎵ h a n g s o cos 20 π 7 t + 7 π 8
+ Hai vật gặp nhau tức là: Δ x → k = 0 lan d a u t = 0 , 15 s

Đáp án A
+ Pha dao động của hai dao động có dạng α = ω t + φ 0 , đồ thị biểu diễn chúng có dạng là hai đường thẳng song song → có cùng hệ số góc, hay nó cách khác là có cùng
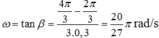
+ Dễ thấy
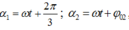
tại t=0,3s thì
![]()
+ Khi hai dao động gặp nhau, ta có
![]()
![]()

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Đáp án B
Ta có:

t = 0 lúc 2 chất điểm đồng thời có mặt tại biên dương nên pha ban đầu của 2 chất điểm đều bằng 0.
Phương trình dao động của 2 vật có dạng: x1 = Acos2πt, x2 = Acos2,5πt
Để 2 chất điểm gặp nhau khi chúng đang chuyển động cùng chiều thì:
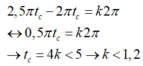
Với k = 1 thì tc = 4s, thay t vào phương trình của x1 và x2 thì ta thấy tại t = 4s hai chất điểm đều ở biên dương, tức chúng đang không chuyển động
→ trong 5 s đầu tiên không có lần nào 2 vật gặp nhau khi đang chuyển động cùng chiều

Đáp án D
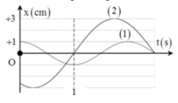
+ Từ đồ thị ta thấy hai dao động có cùng biên độ và
![]()
Tại vị trí hai dao động có cùng li độ
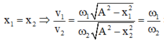
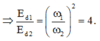

Giải thích: Đáp án D
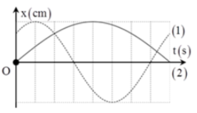
+ Từ đồ thị ta thấy dao động có cùng biên độ và ![]()
Tại vị trí hai dao động có cùng li độ 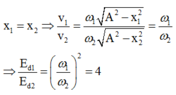

Chọn C


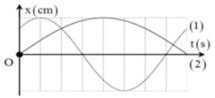
Lúc t = 0 hai chất điểm qua VTCB theo chiều dương (vị trí M 1 , M 2 như hình).
Hai chất điểm gặp nhau ngay sau đó khi chúng ở vị trí M 1 ' , M 2 ' như hình.
![]()
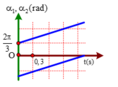
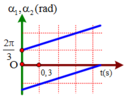




Chọn đáp án A
? Lời giải:
+ Đặt đường trên là dao động (1), đường dưới là dao động (2).
+ Từ đồ thị ta nhận thây hai đường thẳng song song với nhau suy ra ω 2 = ω 1