Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Chọn đáp án A
? Lời giải:
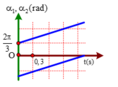
+ Đặt đường trên là dao động (1), đường dưới là dao động (2).
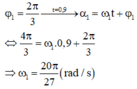
+ Từ đồ thị ta nhận thây hai đường thẳng song song với nhau suy ra ω 2 = ω 1
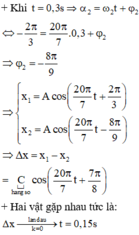

Đáp án A
+ Pha dao động của hai dao động có dạng α = ω t + φ 0 , đồ thị biểu diễn chúng có dạng là hai đường thẳng song song → có cùng hệ số góc, hay nó cách khác là có cùng
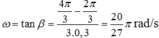
+ Dễ thấy
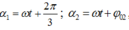
tại t=0,3s thì
![]()
+ Khi hai dao động gặp nhau, ta có
![]()
![]()

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Nhận xét: Thay t =0 vào phương trình vận tốc: v = 4\(\pi\) = vmax
Do vận tốc đạt cực đại, nên vật qua VTCB, nên x = 0.
ta có PT chuẩn: x=Acos(wt+fi); v=-wAsin(wt+fi) => v=wAcos(wt+fi) cụ thể v=4picos(2pit+fi0) hay v=4picos2pit => A=2 mà fi=0 => x được chọn là x=2

Vận tốc cực đại: \(v_{max}=\sqrt{\dfrac{2W_{đmax}}{m}}=\sqrt{\dfrac{2.0,1}{0,2}}=1m/s\)
Khi \(W_{đ1}=0,025J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,025}{0,2}}=0,5m/s\)
Khi \(W_{đ2}=0,75J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,075}{0,2}}=0,5\sqrt 3m/s\)
Vì vận tốc biến thiên điều hoà theo thời gian, nên ta biểu diễn bằng véc tơ quay:
v O 1 0,5 0,5√3 30 0
Từ giản đồ véc tơ ta suy ra được: \(\Delta t=\dfrac{30}{360}T=\dfrac{\pi}{20}\)
\(\Rightarrow T =\dfrac{3\pi}{5}s\)
\(\Rightarrow \omega = \dfrac{2\pi}{T}=\dfrac{10}{3}\) (rad/s)
Biên độ: \(A=\dfrac{v_{max}}{\omega}=0,3m = 30cm\)
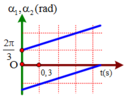
Chọn đáp án A
? Lời giải:
+ Đặt đường trên là dao động (1), đường dưới là dao động (2).
φ 1 = 2 π 3 → t = 0 , 9 α 1 = ω 1 t + φ 1 ⇔ 4 π 3 = ω 1 .0 , 9 + 2 π 3 ⇒ ω 1 = 20 π 27 r a d / s
+ Từ đồ thị ta nhận thây hai đường thẳng song song với nhau suy ra ω 2 = ω 1 .
+ Khi t = 0 , 3 s ⇒ α 2 = ω 2 t + φ 2 ⇔ − 2 π 3 = 20 π 7 .0 , 3 + φ 2 ⇒ φ 2 = − 8 π 9
⇒ x 1 = A cos 20 π 7 t + 2 π 3 x 2 = A cos 20 π 7 t − 8 π 9 ⇒ Δ x = x 1 − x 2 = C ⎵ h a n g s o cos 20 π 7 t + 7 π 8
+ Hai vật gặp nhau tức là: Δ x → k = 0 lan d a u t = 0 , 15 s