Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{R_1}{R_2}=\dfrac{S_2}{S_1}\Rightarrow S_2=\dfrac{R_1.S_1}{R_2}=\dfrac{3.0,4}{6}=0,2\left(mm^2\right)\Rightarrow C\)

Đáp án B
Điện trở tỉ lệ với chiều dài, nên dây 30m có điện trở gấp 3 dây 10m. Vậy R = 3.2 = 6Ω.

Đáp án C
Điện trở tỉ lệ với chiều dài nên 5 / 6 = 15 / l 2 = > l 2 = 15 . 6 / 5 = 18 m

Ta có : 2 dây dẫn cùng tiết tiện và đồng chất => điện trở tỉ lệ thuận với chiều dài => \(\dfrac{R_1}{R_2}=\dfrac{l_1}{l_2}=>\dfrac{3}{6}=\dfrac{6}{l_2}=>l_2=12\left(m\right)\)

Bạn tự làm tóm tắt nhé!
Bài 1:
Tiết diện của dây thứ nhất: \(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p.l}{R}=\dfrac{1,7.10^{-8}.10}{6}\simeq2,9.10^{-8}\)
Điện trở của dây thứ hai: \(R=p\dfrac{l}{S}=1,7.10^{-8}\dfrac{25}{2,9.10^{-8}}\simeq14,7\Omega\)
Bài 2:
Vì tiết diện dây thứ nhất là S1 = 2mm2 bằng \(\dfrac{1}{3}\) lần tiết diện dây thứ hai S2 = 6mm2
→ Điện trở của dây thứ hai nhỏ hơn ba lần điện trở của dây thứ nhất.
Bài 3:
Do điện trở tỉ lệ nghịch với tiết diện của dây dây, ta có:
\(\dfrac{S1}{S2}=\dfrac{R2}{R1}\Rightarrow R_2=R_1\dfrac{S_1}{S_2}=330\dfrac{2,5.10^{-6}}{12,5.10^{-6}}=66\Omega\)

\(\dfrac{R_1}{R_2}=\dfrac{S_2}{S_1}=\dfrac{\dfrac{d_2^2}{4}\pi}{\dfrac{d_1^2}{4}\pi}=\dfrac{d_2^2}{d_1^2}=\dfrac{2}{8}\Rightarrow2d_1^2=8d_2^2\Leftrightarrow d_1=2d_2\)
Chọn D

Ta có: \(\dfrac{R_1}{R_2}=\dfrac{l_1}{l_2}\Rightarrow l_2=\dfrac{R_2.l_1}{R_1}=\dfrac{6.15}{5}=18\left(m\right)\)
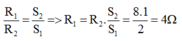
Đáp án A
Điện trở tỉ lệ nghịch với tiết diện:
R 1 / R 2 = S 2 / S 1 = 1 / 3 = > R 1 = R 2 . 1 / 3 = 6 / 3 = 2 Ω