K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 10 2015
ĐK x>= 0
\(F=\frac{x+3\sqrt{x}}{x}=\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{x}=\frac{\sqrt{x}+3}{\sqrt{x}}=1+\frac{3}{\sqrt{x}}\)
Để F nguyên khi \(3\) chia hết cho \(\sqrt{x}\)
=> \(\sqrt{x}\) thuộc ước dương của 3 là { 1 ; 3 }
(+) \(\sqrt{x}=1\Rightarrow x=1\)
(+) \(\sqrt{x}=3\Rightarrow x=9\)
KN
11 tháng 10 2020
Đặt \(a=\sqrt{4+\sqrt{7}}+\sqrt{4-\sqrt{7}}\Rightarrow a^2=8+2\sqrt{\left(4+\sqrt{7}\right)\left(4-\sqrt{7}\right)}=8+6=14\Rightarrow a=\sqrt{14}\)(Dễ thấy a > 0)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2023
Do \(\left\{{}\begin{matrix}x;y;z\ge0\\x+y+z=3\end{matrix}\right.\) \(\Rightarrow0\le x;y;z\le3\)
Đặt \(\left\{{}\begin{matrix}\sqrt{5x+1}=a\\\sqrt{5y+1}=b\\\sqrt{5z+1}=c\end{matrix}\right.\) \(\Rightarrow1\le a;b;c\le4\)
Đồng thời \(a^2+b^2+c^2=5\left(x+y+z\right)+3=18\)
Do \(1\le a\le4\Rightarrow\left(a-1\right)\left(4-a\right)\ge0\Rightarrow5a\ge a^2+4\)
\(\Rightarrow a\ge\dfrac{a^2+4}{5}\)
Tương tự: \(b\ge\dfrac{b^2+4}{5}\) ; \(c\ge\dfrac{c^2+4}{5}\)
Cộng vế: \(a+b+c\ge\dfrac{a^2+b^2+c^2+12}{5}=6\)
\(\Rightarrow A_{min}=6\) khi \(\left(a;b;c\right)=\left(1;1;4\right)\) và hoán vị hay \(\left(x;y;z\right)=\left(0;0;3\right)\) và hoán vị
TC
27 tháng 8 2017
Gọi 1/4 số a là 0,25 . Ta có :
a . 3 - a . 0,25 = 147,07
a . (3 - 0,25) = 147,07 ( 1 số nhân 1 hiệu )
a . 2,75 = 147,07
a = 147,07 : 2,75
a = 53,48
A
1
13 tháng 10 2021
Bài 10:
a: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-8=-2x-3\\y=3x-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-8=-5\end{matrix}\right.\)
Thay x=1 và y=-5 vào (d3), ta được:
\(3m+2m+1=-5\)
hay \(m=-\dfrac{6}{5}\)
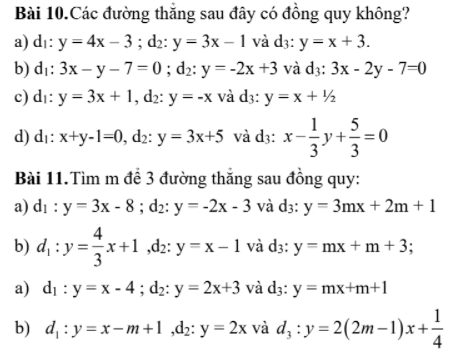
có:
gọi giao điểm nửa đường tròn(H;BH) với AB là G
Ta có:
có: \(\Delta ABC\) vuông tại A\(=>AB^2=BH.BC=>BH=\dfrac{AB^2}{BC}=\dfrac{3^2}{6}=1,5cm=R\)
\(=>S\)(nửa đường tròn tâm H)\(=\dfrac{1}{2}\pi R^2=\dfrac{1}{2}.1,5.\pi=\dfrac{3}{4}.3,14=2,355cm^2\)
xét \(\Delta ABH\) vuông tại H\(=>\sin\angle\left(A\right)=\dfrac{BH}{AB}=\dfrac{1,5}{3}=\dfrac{1}{2}=>\angle\left(A\right)=30^o=>\angle\left(B\right)=60^o\)
xét \(\Delta BHG\) có\(\left\{{}\begin{matrix}HB=HG=R\\\angle\left(B\right)=60^o\end{matrix}\right.\)=>\(\Delta BHG\) đều\(=>S\left(\Delta BHG\right)=R^2.\dfrac{\sqrt{3}}{4}=1,5^2.\dfrac{\sqrt{3}}{4}=\dfrac{9\sqrt{3}}{16}cm^2\)
có: \(S\)(quạt BHG)\(=\dfrac{\pi R^2n^o}{360^o}=\dfrac{3,14.1,5^2.60}{360}=1,1775cm^2\)
có: \(S\left(\Delta ABC\right)=\dfrac{AB.AC}{2}=\dfrac{3\sqrt{6^2-3^2}}{2}=\dfrac{9\sqrt{3}}{2}cm^2\)
\(=>S\)(phần tô đậm)\(=S\left(\Delta ABC\right)-\)[S(nửa đường tròn tâm H)\(-S\)(quạt tròn BHG-\(S\left(\Delta BHG\right)\)]
(bạn tự thay vào đi)