
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2

Bạn nên chịu khó gõ đề ra khả năng được giúp sẽ cao hơn.
Câu h của em đây nhé
h, ( 1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1 - \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3-\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{2}\)
= -2

Điều kiện \(0\le x\le1\)
\(A=2014\sqrt{x}+2015\sqrt{1-x}\)
\(=2014\left(\sqrt{x}+\sqrt{1-x}\right)+\sqrt{1-x}\)
Ta có:
\(\sqrt{x}+\sqrt{1-x}\ge\sqrt{x+1-x}=1\)
Và \(x\le1\Leftrightarrow1-x\ge0\)
Từ đây ta có
\(A\ge2014.1+0=2014\)
Vậy GTNN của A = 2014 đạt được khi x = 1

Em dùng công thức toán học hoặc viết ra giấy, chụp ảnh rồi up lên chứ thế này cô không đúng đề bài để giúp em được.

https://vndoc.com/mot-so-bai-tap-toan-nang-cao-lop-9/download
http://h7.net/tu-lieu/toan-nang-cao/toan-nang-cao-lop-9/
https://download.com.vn/docs/mot-so-bai-tap-toan-nang-cao-lop-9/download
https://toancap2.com/toan-9/boi-duong-toan-9/...............................


\(B=\dfrac{1}{\sqrt{3}-2}-\dfrac{1}{\sqrt{3}+2}\)
\(=\dfrac{\sqrt{3}+2-\left(\sqrt{3}-2\right)}{\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)}\)
\(=\dfrac{\sqrt{3}+2-\sqrt{3}+2}{3-4}=\dfrac{4}{-1}=-4\)
\(C=\sqrt{8-2\sqrt{15}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot\sqrt{3}+3}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-\sqrt{5}\)
\(=\sqrt{5}-\sqrt{3}-\sqrt{5}=-\sqrt{3}\)
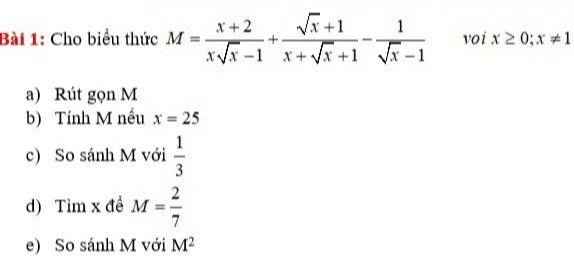



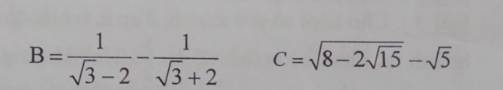
`a)M=(x+2)/(xsqrtx-1)+(sqrtx+1)/(x+sqrtx+1)-1/(sqrtx-1)(x>=0,x ne 1)`
`M=(x+2)/((sqrtx-1)(x+sqrtx+1))+((sqrtx+1)(sqrtx-1))/((sqrtx-1)(x+sqrtx+1))-(x+sqrtx+1)/((sqrtx-1)(x+sqrtx+1))`
`M=(x+2+x-1-x-sqrtx-1)/((sqrtx-1)(x+sqrtx+1))`
`M=(x-sqrtx)/((sqrtx-1)(x+sqrtx+1))`
`M=(sqrtx(sqrtx-1))/((sqrtx-1)(x+sqrtx+1))`
`M=sqrtx/(x+sqrtx+1)`
`b)x=25(tmđk)`
`=>sqrtx=5`
`=>M=5/(25+5+1)`
`=>M=5/31`
`c)M=sqrtx/(x+sqrtx+1)`
`x=0=>M=0<1/3`
`x>0=>M=1/(sqrtx+1+1/sqrtx)`
Áp dụng bđt cosi:
`sqrtx+1/sqrtx>=2`
`=>sqrtx+1+1/sqrtx>=3>0`
`=>M<=1/3`
Dấu "=" xảy ra khi `sqrtx=1/sqrtx<=>x=1`(KTMĐKXĐ)
`=>M<1/3`
Vậy `M<1/3`
`d)M=2/7`
`<=>sqrtx/(x+sqrtx+1)=2/7`
`<=>2x+2sqrtx+2=7`
`<=>2x-5sqrtx+2=0`
`<=>2x-4sqrtx-sqrtx+2=0`
`<=>(sqrtx-2)(2sqrtx-1)=0`
`<=>[(sqrtx=2),(2sqrtx=1):}`
`<=>[(x=4),(x=1/4):}(TMĐK)`
`e)` Vì `x>=0=>sqrtx>=0`
`=>x+sqrtx+1>=1>0`
`=>M>=0`
Mặt khác:`M<1/3`(câu b)
`=>M<1=>M-1<0`
`=>M(M-1)<=0`
`<=>M^2-M<=0`
`<=>M^2<=M`
a: Ta có: \(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
b: Thay x=25 vào M, ta được:
\(M=\dfrac{5}{25+5+1}=\dfrac{5}{31}\)
c: Ta có: \(M-\dfrac{1}{3}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{3}\)
\(=\dfrac{3\sqrt{x}-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(x-2\sqrt{x}+1\right)}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(\sqrt{x}-1\right)^2}{3\left(x+\sqrt{x}+1\right)}< 0\forall x\) thỏa mãn ĐKXĐ
hay \(M< \dfrac{1}{3}\)