
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


AB/MN=AC/MP=BC/NP
=>5/4=MP/8=NP/6
=>MP=10cm; NP=7,5cm


Câu 3:
Gọi số học sinh khối 8 và số học sinh khối 9 lần lượt là a,b
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=500\\\dfrac{9}{20}a+\dfrac{2}{5}b=213\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=260\\b=240\end{matrix}\right.\)

Lời giải:
a.
Tứ giác $ADME$ có 3 góc vuông: $\widehat{D}=\widehat{A}=\widehat{E}=90^0$ nên là hình chữ nhật.
b.
Vì $ADME$ là hcn nên $AM=DE$
$MD\perp AB, AB\perp AC\Rightarrow MD\parallel AC$. Áp dụng định lý Talet:
$\frac{BD}{DA}=\frac{BM}{MC}=1\Rightarrow BD=DA\Rightarrow D$ là trung điểm $AB$
Tương tự thì $E$ là trung điểm $AC$
$\Rightarrow DE$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow AM=DE=\frac{BC}{2}=\frac{\sqrt{AB^2+AC^2}}{2}=\frac{\sqrt{6^2+8^2}}{2}=5$ (cm)
c.
$S_{AMB}=\frac{BM}{BC}S_{ABC}=\frac{1}{2}S_{ABC}=\frac{1}{2}.\frac{AB.AC}{2}=\frac{6.8}{4}=12$ (cm2)
Điểm H ở đây có vẻ không có giá trị lắm.

1: Xét tứ giác AHBE có
M là trung điểm của AB
M là trung điểm của HE
Do đó: AHBE là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBE là hình chữ nhật



Bài 4:
a) Xét ΔABC có
M là trung điểm của BC
MN//AC
Do đó: N là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
N là trung điểm của AB
Do đó: MN là đường trung bình của ΔABC
Suy ra: \(MN=\dfrac{AC}{2}\)
hay AC=2MN
b) Xét ΔABC có
M là trung điểm của BC
MP//AB
Do đó: P là trung điểm của AC
Xét ΔABC có
M là trung điểm của BC
P là trung điểm của AC
Do đó: MP là đường trung bình của ΔABC
Suy ra: \(MP=\dfrac{AB}{2}\)
mà \(BN=\dfrac{AB}{2}\)
nên MP=BN
Xét tứ giác BMPN có
MP//NB(cmt)
PM=NB(cmt)
Do đó: BMPN là hình bình hành
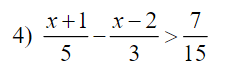


 giải giúp mình câu 4 với
giải giúp mình câu 4 với 



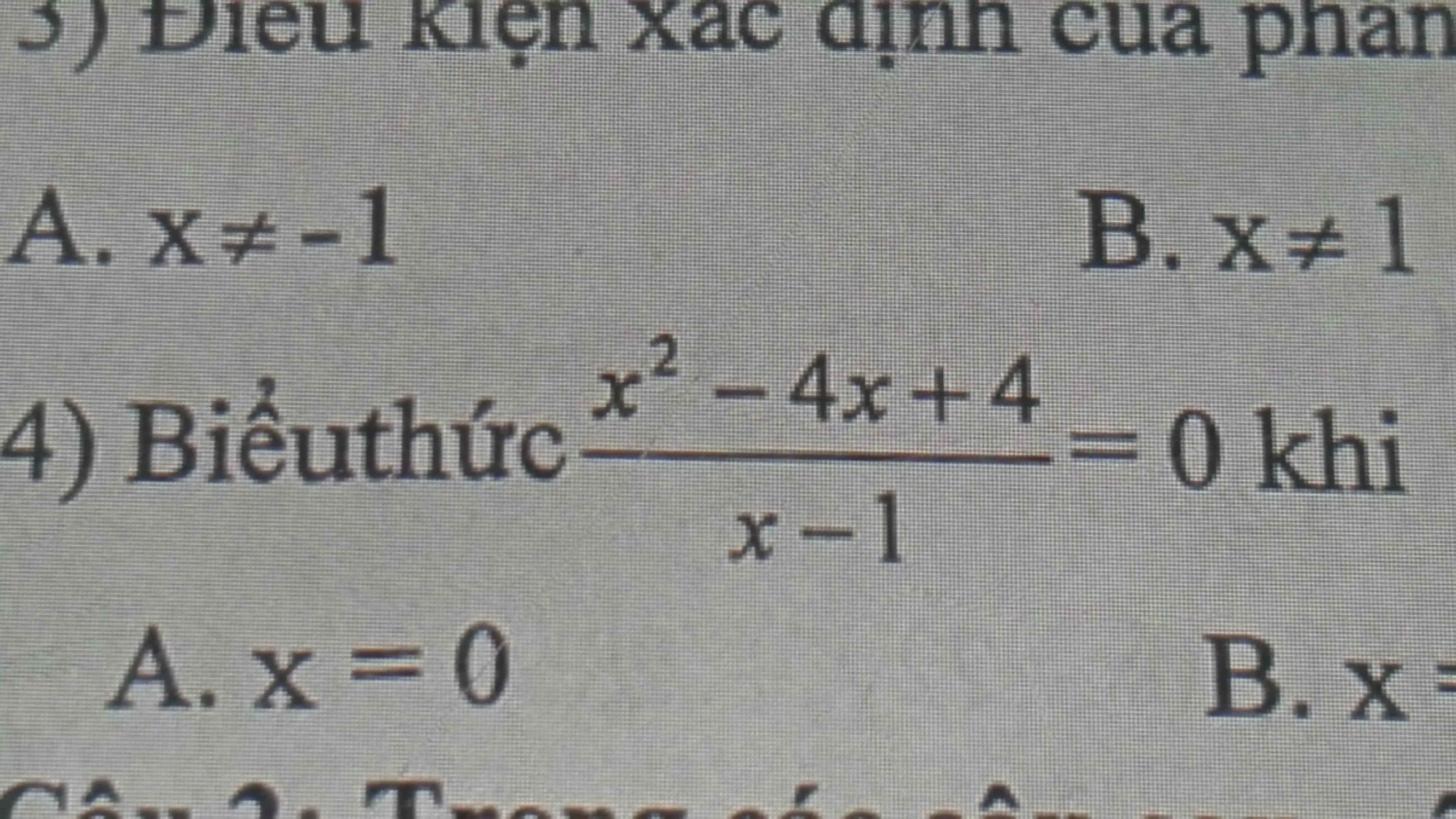

\(\Leftrightarrow\dfrac{3\left(x+1\right)-5\left(x-2\right)}{15}>\dfrac{7}{15}\)
\(\Leftrightarrow3\left(x+1\right)-5\left(x-2\right)>7\)
\(\Leftrightarrow3x+3-5x+10>7\)
\(\Leftrightarrow-2x>-6\)
\(\Leftrightarrow x< 3\)
Vậy \(S=\left\{x|x< 3\right\}\)