K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
=)))
0
CC
3
2 tháng 12 2016
Ta có : A = 1.2 + 2.3 + 3.4 + … + n.(n + 1)
\(\Rightarrow\)3A = 1.2.(3-0)+2.3.(4-1)+3.4.(5-2).....n.(n+1).[(n+2)-(n-1)]
\(\Rightarrow\)3A= 1.2.3-0.1.2+2.3.4-1.2.3+3.4.5-2.3.4+4.5.6-3.4.5+....+n.(n+1)(n+2)-(n-1)n(n+1)
\(\Rightarrow\)3A= (1.2.3-1.2.3)+(2.3.4-2.3.4)+....+[(n-1).n.(n+1)-(n-1)n(n+1)]+n.(n+1)(n+2)
\(\Rightarrow\)3A=n.(n+1)(n+2)
\(\Rightarrow\)A=\(\frac{\text{n.(n+1)(n+2)}}{3}\)
2D
3
15 tháng 10 2021
\(c,\Leftrightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{6};2x+y=14\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{6}=\dfrac{2x+y}{4+3}=\dfrac{14}{7}=2\\ \Leftrightarrow\left\{{}\begin{matrix}x=4\\y=6\\z=12\end{matrix}\right.\)
\(d,\dfrac{x}{2}=\dfrac{y}{3}\Leftrightarrow\dfrac{x}{10}=\dfrac{y}{15};\dfrac{y}{5}=\dfrac{z}{7}\Leftrightarrow\dfrac{y}{15}=\dfrac{z}{21}\\ \Leftrightarrow\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{98}{46}=2\\ \Leftrightarrow\left\{{}\begin{matrix}x=20\\y=30\\z=42\end{matrix}\right.\)
TT
15 tháng 10 2021
Bài 2:
giải:gọi số hs của 3 tổ lần lượt là a,b,c(a,b,c >0)
Theo bài ra ,ta có:
a/2=b/3=c/4 và a+b+c=45
áp dụng tính chất dãy tỉ số bằng nhau:
a/2=b/3=c/4=a+b+c/2+3+4=45/9=5
Vậy a=5.2=10
b=5.3=15
c=5.4=20
Câu 3:
giải:gọi số hs thích các môn lần lượt là a,b,c(a,b,c >0)
Theo bài ra ta có:
a/2=b/3=c/5 và c-a=6
áp dụng tính chất dãy tỉ số bằng nhau ta có:
a/2=b/3=c/5=c-a/-2=6/3=2
Vậy a=2.2=4
b=2.3=6
c=2.5=10
M
3
2D
0
15 tháng 3 2021
Ta có: x=2018
nên x+1=2019
Ta có: \(A=x^5-2019x^4+2019x^3-2019x^2+2019x-2020\)
\(=x^5-x^4\left(x+1\right)+x^3\left(x+1\right)-x^2\left(x+1\right)+x\left(x+1\right)-2020\)
\(=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x-2020\)
\(=x-2020=2019-2020=-1\)
ND
0
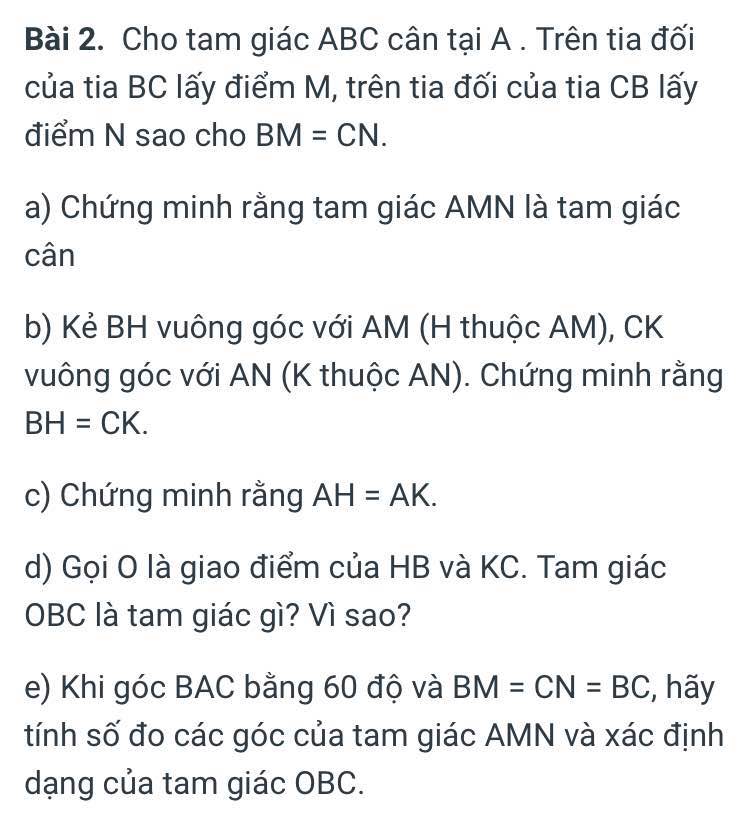
a. xét tam giác ABM và tam giác ACN, có:
AB = AC ( ABC cân )
góc ABM = góc ACN ( 2 góc ngoài của tam giác cân )
BM = CN ( gt )
Vậy tam giác ABM = tam giác ACN ( c.g.c )
b. xét tam giác vuông ABH và tam giác vuông ACK, có:
AB = AC ( ABC cân )
góc MAB = góc NAC ( tam giác ABM = tam giác ACN )
Vậy tam giác vuông ABH = tam giác vuông ACK ( cạnh huyền.góc nhọn )
=> BH = CK ( 2 cạnh tương ứng )
c. ta có: tam giác vuông ABH = tam giác vuông ACK
=> AH = AK ( 2 cạnh tương ứng )
d. ta có: góc OBC = góc OCB
=> tam giác OBC cân tại O
e. ta có AB = AC mà A = 60 độ
=> ABC là tam giác đều
Mà BM = CN = BC , BC lại = AB
=> BM = CN = AB
Mà góc AMB = góc ANC ( cmt )
=> tam giác AMN là tam giác đều ( BM = CN và góc AMB = góc ANC )
Tham khảo:
a) tam giác ABC cân
=> góc ABC=góc ACB
góc MBA+góc ABC=180độ (kề bù)
góc NCA+góc ACB=180độ(kề bù)
=> góc ABM=góc ACN
xét 2 tam giác ABM và ACN có:
AB=AC(tam giác ABC cân )
góc ABM=góc ACN(chứng minh trên)
BM=CN(gt)
=> 2 tam giác ABM=ACN(c.g.c)
=> AM=AN(2 cạnh tương ứng)
=> tam giác AMN cân ở A
b) tam giác AMN cân ở A
=> góc M=góc N
xét 2 tam giác MHB và NKC có:
góc MHB=góc NKC(=90độ)
MB=NC(gt)
góc M =góc N(chứng minh trên)
=> 2 tam giác MHB=NKC(cạnh huyền - góc nhọn)
=> BH=CK(2 cạnh tương ứng)
c) ta có : AM=AN (theo a)
HM=KN (tam giác MHB=tam giác NKC)
AM = AH+HM
AN= AK+ KN
=> AH= AK
d) tam giác MHB=tam giác NKC(theo b)
=> góc HBM=góc KCN(2 góc tương ứng)
góc HBM=góc OBC(đối đỉnh)
góc KCN=góc OCB(đối đỉnh)
=> góc OBC=góc OCB
=> tam giác OBC cân ở O
e) tam giác ABC có AB=AC ; góc BAC=60độ
=> tam giác ABC đều
=> AB=AC=BC
mà BC=BM(gt)
=> BM=AB
=>tam giác ABM cân ở B
góc ABC + góc ABM=180độ (kề bù)
=> góc ABM =180độ - góc ABC
=180độ-60độ
=120độ
tam giác ABC cân ở B
=> góc BAM=góc BMA =(180độ-góc ABM) / 2=180−120/2=60/2=30 độ
vậy góc AMN=30độ