
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) \(A=10^{100}+5\)
- Tận cùng A là số 5 \(\Rightarrow A⋮5\)
- Tổng các chữ số của A là \(1+5=6⋮3\Rightarrow A⋮3\) \(\)
\(\Rightarrow dpcm\)
b) \(B=10^{50}+44\)
- Tận cùng B là số 4 là số chẵn \(\Rightarrow B⋮2\)
- Tổng các chữ số của B là \(1+4+4=9⋮9\Rightarrow B⋮9\)
\(\Rightarrow dpcm\)

Hiệu số phần bằng nhau là :
5 - 3 = 2 ( phần )
Tử số của phân số đó là :
8 : 2 x 5 = 20
Mẫu số của phân số đó là :
20 : 5 x 3 = 12
Vậy phân số cần tìm là \(\frac{20}{12}\)
Gọi x là tử số
mẫu số là x - 8
Theo đề , ta có
\(\frac{x}{x-8}=\frac{5}{3}\left(x\ne8\right)\)
\(x\cdot3=5\cdot\left(x-8\right)\)
\(3x=5x-40\)
\(40=5x-3x\)
\(40=2x\)
\(x=20\)
vậy phân số cần tìm là \(\frac{20}{12}\)

Answer:
\(\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{3}{8}+...+\dfrac{10}{2^{10}}\)
\(=\left(\dfrac{2}{2^0}-\dfrac{3}{2^1}\right)+\left(\dfrac{3}{2^1}-\dfrac{4}{2^2}\right)+\left(\dfrac{4}{2^2}+\dfrac{5}{2^3}\right)+...+\left(\dfrac{11}{2^9}-\dfrac{12}{2^{10}}\right)\)
\(=2-\dfrac{12}{2^{10}}\)
\(=2-\dfrac{3}{256}\)
\(=\dfrac{512}{256}-\dfrac{3}{256}\)
\(=\dfrac{509}{256}\)
*Để làm bài này dễ hơn, bạn áp dụng công thức sau:
\(\dfrac{n}{2^n}=\dfrac{n+1}{2^{n-1}}-\dfrac{n+2}{2^n}\)

3: \(\Leftrightarrow x\cdot\dfrac{-3}{5}=\dfrac{1}{4}+\dfrac{3}{4}=1\)
nên x=-5/3
4: \(\Leftrightarrow x\cdot\dfrac{4}{28}=\dfrac{28}{3}\cdot\dfrac{3}{28}=1\)
hay x=28/4=7
5: \(\Leftrightarrow x:\left(\dfrac{7}{2}-\dfrac{31}{6}\right)=\dfrac{21}{5}-\dfrac{20}{3}\)
\(\Leftrightarrow x:\dfrac{-5}{3}=\dfrac{-37}{15}\)
\(\Leftrightarrow x=\dfrac{37}{15}\cdot\dfrac{5}{3}=\dfrac{37}{9}\)

c: \(=\dfrac{-27\cdot100}{-30}=\dfrac{2700}{30}=90\)



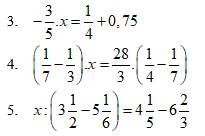 giúp mik với ạ. cảm ơn ạ
giúp mik với ạ. cảm ơn ạ
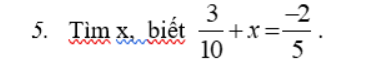 Giúp mik với ạ mik cần gấp lắm cảm ơn nhìu!
Giúp mik với ạ mik cần gấp lắm cảm ơn nhìu!
\(A=\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{3}{8}+...+\dfrac{10}{2^{10}}\)
\(2A=\dfrac{1}{1}+\dfrac{2}{2}+\dfrac{3}{4}+...+\dfrac{10}{2^9}\)
\(2A-A=\left(1+\dfrac{2}{2}+\dfrac{3}{4}+...+\dfrac{10}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{2}{4}+...+\dfrac{10}{2^{10}}\right)\)
\(A=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}-\dfrac{10}{2^{10}}\)
\(B=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}\)
\(2B=2+1+\dfrac{1}{2}+...+\dfrac{1}{2^8}\)
\(2B-B=\left(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^8}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}\right)\)
\(B=2-\dfrac{1}{2^9}\)
Suy ra \(A=B-\dfrac{10}{2^{10}}=2-\dfrac{1}{2^9}-\dfrac{10}{2^{10}}=\dfrac{509}{256}\)