
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2

Lời giải:
ĐKXĐ: $x\geq 0; x\neq 1$
a.
\(A=\left[\frac{x+2}{(\sqrt{x}-1)(x+\sqrt{x}+1)}+\frac{\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}-1)(x+\sqrt{x}+1)}-\frac{x+\sqrt{x}+1}{(\sqrt{x}-1)(x+\sqrt{x}+1)}\right].\frac{2}{\sqrt{x}-1}\)
\(=\frac{x+2+x-\sqrt{x}-(x+\sqrt{x}+1)}{(\sqrt{x}-1)(x+\sqrt{x}+1)}.\frac{2}{\sqrt{x}-1}\)
\(=\frac{2(x-2\sqrt{x}+1)}{(\sqrt{x}-1)^2(x+\sqrt{x}+1)}=\frac{2(\sqrt{x}-1)^2}{(\sqrt{x}-1)^2(x+\sqrt{x}+1)}=\frac{2}{x+\sqrt{x}+1}\)
b.
Ta thấy với $x\geq 0 ; x\neq 1$ thì $x+\sqrt{x}+1\geq 1$
$\Rightarrow A=\frac{2}{x+\sqrt{x}+1}\leq 2$
Vậy $A$ đạt max bằng $2$ khi $x=0$

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề hơn.

1: \(A=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-5-\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-4-\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{x-\sqrt{x}-12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)

\(M=\left(\dfrac{\sqrt{x}}{2x}-\dfrac{1}{\sqrt{x}}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\\ =\left(\dfrac{\sqrt{x}}{2x}-\dfrac{2\sqrt{x}}{2x}\right)\cdot\left(\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\dfrac{x-2\sqrt{x}}{2x}\cdot\dfrac{x-2\sqrt{x}+1-\left(x+2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-2\right)}{x-1}\)

a) \(P=\left(3-\dfrac{3}{\sqrt{x}-1}\right):\left(\dfrac{x+2}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}+2}\right)\)
\(=\left(\dfrac{3\left(\sqrt{x}-1\right)-3}{\sqrt{x}-1}\right):\left[\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x+2}\right)}-\dfrac{\sqrt{x}}{\sqrt{x}+2}\right]\)
\(=\dfrac{3\sqrt{x}-3-3}{\sqrt{x}-1}:\dfrac{x+2-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\sqrt{x}-1}:\dfrac{x+2-x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\sqrt{x}-1}:\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\sqrt{x}-1}:\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{3\sqrt{x}-6}{\sqrt{x}-1}.\left(\sqrt{x}-1\right)\)
\(=3\sqrt{x}-6\)
b) \(P=\dfrac{4\sqrt{x}-1}{\sqrt{x}}\)
\(\Leftrightarrow3\sqrt{x}-6=\dfrac{4\sqrt{x}-1}{\sqrt{x}}\) (1)
ĐKXĐ: \(x>0\)
\(\left(1\right)\Leftrightarrow3x-6\sqrt{x}=4\sqrt{x}-1\)
\(\Leftrightarrow3x-6\sqrt{x}-4\sqrt{x}+1=0\)
\(\Leftrightarrow3x-10\sqrt{x}+1=0\) (2)
Đặt \(t=\sqrt{x}\ge0\)
\(\left(2\right)\Leftrightarrow3t^2-10t+1=0\)
\(\Delta'=25-4=22\)
Phương trình có hai nghiệm phân biệt:
\(t_1=\dfrac{5+\sqrt{22}}{3}\) (nhận)
\(t_2=\dfrac{5-\sqrt{22}}{3}\) (nhận)
Với \(t=\dfrac{5+\sqrt{22}}{3}\) \(\Leftrightarrow\sqrt{x}=\dfrac{5+\sqrt{22}}{3}\Leftrightarrow x=\dfrac{47+10\sqrt{22}}{9}\) (nhận)
Với \(t=\dfrac{5-\sqrt{22}}{3}\Leftrightarrow\sqrt{x}=\dfrac{5-\sqrt{22}}{3}\Leftrightarrow x=\dfrac{47-10\sqrt{22}}{9}\) (nhận)
Vậy \(x=\dfrac{47+10\sqrt{22}}{9};x=\dfrac{47-10\sqrt{22}}{9}\) thì \(P=\dfrac{4\sqrt{x}-1}{\sqrt{x}}\)
a: \(P=\dfrac{3\sqrt{x}-3-3}{\sqrt{x}-1}:\dfrac{x+2-x+\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}=3\sqrt{x}-6\)
b: P=(4căn x-1)/căn x
=>3x-6căn x-4căn x+1=0
=>3x-10căn x+1=0
=>x=(47+10căn 22)/9 hoặc x=(47-10căn 22)/9

\(15,A=\dfrac{x-1-4\sqrt{x}+4+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ A=\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\\ 16,B=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{2\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\\ B=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-2\left(\sqrt{x}+1\right)+2\left(\sqrt{x}+1\right)\\ B=x-\sqrt{x}-2\sqrt{x}-2+2\sqrt{x}+2=x-\sqrt{x}\)

15. \(=\dfrac{x-1-4\left(\sqrt{x}-1\right)+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{x-4\sqrt{x}+4}{x-1}.\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\left(\sqrt{x}-2\right)^2.\dfrac{1}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
 giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.
giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.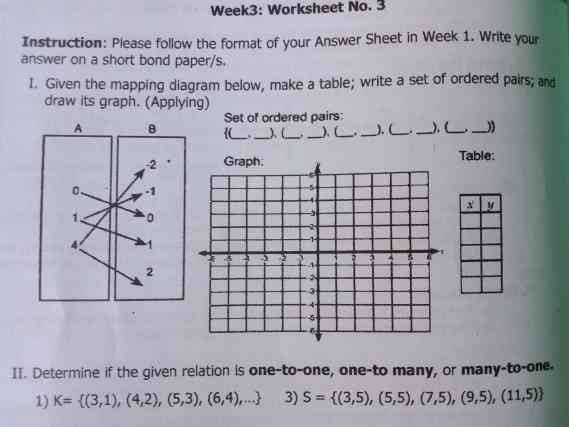

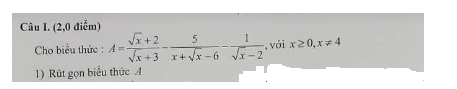 rút gọn biểu thức, giúp e với ạ :<
rút gọn biểu thức, giúp e với ạ :<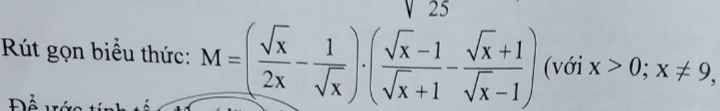


bn gửi lại cho rõ hơn đi. chơ ảnh này mờ quá