
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e: \(\left(-4156+2021\right)-\left(119+2021-4156\right)\)
\(=-4156+2021-119-2021+4156\)
\(=\left(-4156+4156\right)+\left(2021-2021\right)-119\)
=0+0-119
=-119
g: \(315\cdot75-\left(15\cdot100-315\cdot25\right)\)
\(=315\cdot75-15\cdot100+315\cdot25\)
\(=315\left(75+25\right)-15\cdot100\)
\(=315\cdot100-15\cdot100=300\cdot100=30000\)
h: \(\left(-489\right)\cdot125-\left(125\cdot11-500\cdot25\right)\)
\(=-489\cdot125-125\cdot11+500\cdot25\)
\(=125\left(-489-11\right)+500\cdot25\)
\(=125\cdot\left(-500\right)+500\cdot25\)
\(=500\left(-125+25\right)\)
\(=500\cdot\left(-100\right)=-50000\)
Bài 2:
a: \(-415-3\left(2x-1\right)^2=-490\)
=>\(3\left(2x-1\right)^2+415=490\)
=>\(3\left(2x-1\right)^2=75\)
=>\(\left(2x-1\right)^2=25\)
=>\(\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

z4:
\(\dfrac{24}{148}=\dfrac{6}{37}=\dfrac{108}{37\cdot18}\)
\(\dfrac{-14}{-36}=\dfrac{7}{18}=\dfrac{7\cdot37}{18\cdot37}=\dfrac{259}{37\cdot18}\)
mà 108<259
nên \(\dfrac{24}{148}< \dfrac{-14}{-36}\)
z5: \(\dfrac{-26}{-72}=\dfrac{26}{72}< 1\)
\(1< \dfrac{45}{20}=\dfrac{-45}{-20}\)
Do đó: \(\dfrac{-26}{-72}< \dfrac{-45}{-20}\)
z6: \(\dfrac{14}{42}=\dfrac{1}{3}=\dfrac{1\cdot4}{3\cdot4}=\dfrac{4}{12}\)
\(\dfrac{21}{28}=\dfrac{3}{4}=\dfrac{3\cdot3}{4\cdot3}=\dfrac{9}{12}\)
mà 4<9
nên \(\dfrac{14}{42}< \dfrac{21}{28}\)
z7: \(\dfrac{-14}{-56}=\dfrac{1}{4}=\dfrac{5}{20}\)
\(\dfrac{21}{35}=\dfrac{3}{5}=\dfrac{3\cdot4}{5\cdot4}=\dfrac{12}{20}\)
mà 5<12
nên \(\dfrac{-14}{-56}< \dfrac{21}{35}\)
z8: \(10A=\dfrac{10^{201}+10}{10^{201}+1}=1+\dfrac{9}{10^{201}+1}\)
\(10B=\dfrac{10^{202}+10}{10^{202}+1}=1+\dfrac{9}{10^{202}+1}\)
\(10^{201}+1< 10^{202}+1\)
=>\(\dfrac{9}{10^{201}+1}>\dfrac{9}{10^{202}+1}\)
=>\(\dfrac{9}{10^{201}+1}+1>\dfrac{9}{10^{202}+1}+1\)
=>10A>10B
=>A>B

a: \(248\left(13-197\right)+197\left(248-13\right)\)
\(=248\cdot13-248\cdot197+197\cdot248-197\cdot13\)
\(=248\cdot13-197\cdot13\)
\(=51\cdot13=663\)
b: \(146\left(295-39\right)-295\left(146-39\right)\)
\(=146\cdot295-146\cdot39-295\cdot146+295\cdot39\)
\(=295\cdot39-146\cdot39\)
\(=39\cdot149=5811\)
c: \(\left(-245\right)\left(45-948\right)-45\left(948-245\right)\)
\(=-245\cdot45+245\cdot948-45\cdot948+45\cdot245\)
\(=245\cdot948-45\cdot948\)
\(=200\cdot948=189600\)
d: \(\left(-3\right)^4-7\cdot\left(-2\right)\cdot\left(-3\right)^3+4^3-\left(-2024\right)^0\)
\(=81+14\cdot\left(-27\right)+64-1\)
\(=144-378=-234\)

55:
Chiều rộng mảnh vườn là \(56\cdot\dfrac{5}{8}=35\left(m\right)\)
Chu vi mảnh vườn là \(\left(56+35\right)\cdot2=182\left(m\right)\)
Diện tích mảnh vườn là \(56\cdot35=1960\left(m^2\right)\)
56:
Ngày thứ nhất trồng được \(56\cdot\dfrac{3}{8}=7\cdot3=21\left(cây\right)\)
Số cây còn lại cần trồng là:
56-21=35(cây)
Ngày 2 trồng được \(35\cdot\dfrac{4}{7}=20\left(cây\right)\)

d: Ta có: ƯCLN(a,b)=2
=>\(\left\{{}\begin{matrix}a=2x\\b=2y\end{matrix}\right.\)
\(a\cdot b=120\)
=>\(2x\cdot2y=120\)
=>\(x\cdot y=30\)
mà x,y là các số nguyên dương
nên \(\left(x,y\right)\in\left\{\left(1;30\right);\left(2;15\right);\left(3;10\right);\left(5;6\right);\left(6;5\right);\left(10;3\right);\left(15;2\right);\left(30;1\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(2;60\right);\left(4;30\right);\left(6;20\right);\left(10;12\right);\left(12;10\right);\left(20;6\right);\left(30;4\right);\left(60;2\right)\right\}\)

p: \(\left(-\dfrac{2}{5}\right)^2+\dfrac{17}{-18}\cdot\dfrac{36}{34}-\left(-\dfrac{2}{3}\right)^3\)
\(=\dfrac{4}{25}-\dfrac{17}{34}\cdot\dfrac{36}{18}-\dfrac{-8}{27}\)
\(=\dfrac{4}{25}+\dfrac{8}{27}-1=\dfrac{-367}{675}\)
q: \(\left(-\dfrac{1}{2}\right)^0-\dfrac{-1}{3}\cdot\dfrac{-9}{12}+\dfrac{2^4}{-4}\)
\(=1-\dfrac{1}{3}\cdot\dfrac{3}{4}+\dfrac{16}{-4}\)
\(=1-\dfrac{1}{4}-4=-3-\dfrac{1}{4}=-\dfrac{13}{4}\)
r: \(\left(-5\right)\cdot\dfrac{17}{45}-\left(-\dfrac{2}{3}\right)^2+\left(-\dfrac{20}{2023}\right)^0\)
\(=-\dfrac{17}{9}-\dfrac{4}{9}+1\)
\(=-\dfrac{21}{9}+1=-\dfrac{12}{9}=-\dfrac{4}{3}\)


ƯC của(−15;+20) là: {±1;±5}
đây là theo hiểu biết của mk thôi nha, ko chép ai đâu^^

a)
\(\frac{x-3}{10}=\frac{4}{x-3}\)
=> ( x - 3 )2 = 4 . 10.
( x - 3 )2 = 40
Mà x - 3 thuộc Z ( vì x thuộc Z ) nên ( x - 3 )2 là số chính phương.
Do 40 không là số chính phương.
=> Ko tìm được x thuộc Z thỏa mãn đề bài.
b)
\(\frac{x+5}{9}=\frac{4}{x+5}\)
=> ( x + 5 )2 = 4 . 9
( x + 5 )2 = 36
=> x + 5 = 6 hoặc x + 5 = -6.
+) x + 5 = 6
x = 1.
+) x + 5 = -6
x = -11.
Vậy x = 1; x = -11.
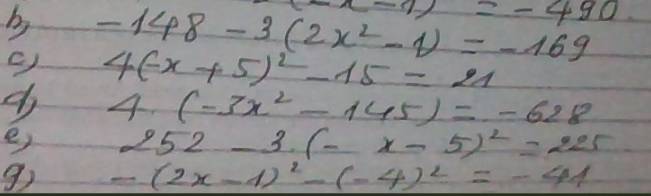
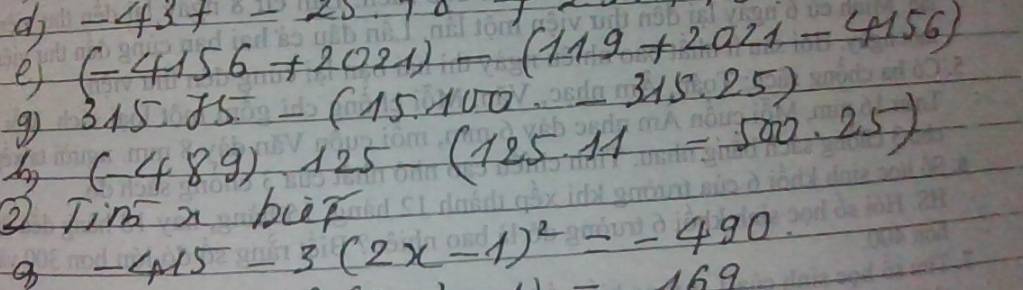

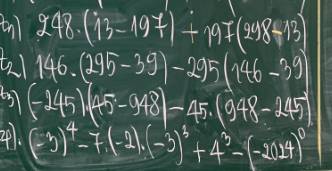

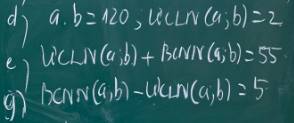
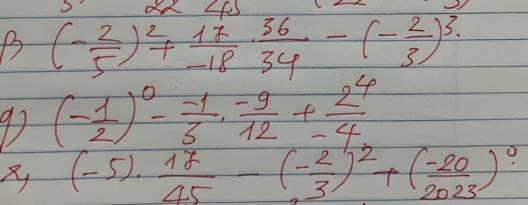
Lời giải:
b. $-138-3(2x^2-1)=-169$
$3(2x^2-1)=-148-(-169)=21$
$2x^2-1=21:3=7$
$2x^2=7+1=8$
$x^2=4=2^2=(-2)^2\Rightarrow x=\pm 2$
c.
$4(-x+5)^2-15=21$
$4(-x+5)^2=21+15=36$
$(-x+5)^2=36:4=9=3^2=(-3)^2$
$\Rightarrow -x+5=3$ hoặc $-x+5=-3$
$\Rightarrow x=2$ hoặc $x=8$
d.
$4(-3x^2-145)=-628$
$-3x^2-145=-628:4=-157$
$3x^2+145=157$
$3x^2=157-145=12$
$x^2=12:3=4=2^2=(-2)^2$
$\Rightarrow x=\pm 2$
e.
$252-3(-x-5)^2=225$
$3(-x-5)^2=252-225=27$
$(-x-5)^2=27:3=9$
$(x+5)^2=3^2=(-3)^2$
$\Rightarrow x+5=3$ hoặc $x+5=-3$
$\Rightarrow x=-2$ hoặc $x=-8$