
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d: Ta có: ƯCLN(a,b)=2
=>\(\left\{{}\begin{matrix}a=2x\\b=2y\end{matrix}\right.\)
\(a\cdot b=120\)
=>\(2x\cdot2y=120\)
=>\(x\cdot y=30\)
mà x,y là các số nguyên dương
nên \(\left(x,y\right)\in\left\{\left(1;30\right);\left(2;15\right);\left(3;10\right);\left(5;6\right);\left(6;5\right);\left(10;3\right);\left(15;2\right);\left(30;1\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(2;60\right);\left(4;30\right);\left(6;20\right);\left(10;12\right);\left(12;10\right);\left(20;6\right);\left(30;4\right);\left(60;2\right)\right\}\)

Bài 19:
Chu vi hình vuông là: \(\left(12+6\right)\cdot2=36\left(cm\right)\)
Độ dài cạnh hình vuông là 36/4=9(cm)
Diện tích hình vuông là \(9^2=81\left(cm^2\right)\)
Bài 20:
Độ dài đường cao là \(\dfrac{160}{4}=40\left(m\right)\)
Diện tích miếng đất là: \(60\cdot40=2400\left(m^2\right)=0,24\left(ha\right)\)
Khối lượng ngô thu hoạch được là:
\(0,24:3\cdot13,5=1,08\left(tấn\right)=1080\left(kg\right)\)

a: \(248\left(13-197\right)+197\left(248-13\right)\)
\(=248\cdot13-248\cdot197+197\cdot248-197\cdot13\)
\(=248\cdot13-197\cdot13\)
\(=51\cdot13=663\)
b: \(146\left(295-39\right)-295\left(146-39\right)\)
\(=146\cdot295-146\cdot39-295\cdot146+295\cdot39\)
\(=295\cdot39-146\cdot39\)
\(=39\cdot149=5811\)
c: \(\left(-245\right)\left(45-948\right)-45\left(948-245\right)\)
\(=-245\cdot45+245\cdot948-45\cdot948+45\cdot245\)
\(=245\cdot948-45\cdot948\)
\(=200\cdot948=189600\)
d: \(\left(-3\right)^4-7\cdot\left(-2\right)\cdot\left(-3\right)^3+4^3-\left(-2024\right)^0\)
\(=81+14\cdot\left(-27\right)+64-1\)
\(=144-378=-234\)

h: \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{9\cdot10}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=1-\dfrac{1}{10}=\dfrac{9}{10}\)
m: \(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
\(=\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
\(=\dfrac{1}{2}-\dfrac{1}{8}=\dfrac{3}{8}\)

v: \(\dfrac{26}{-37}< 0\)
\(0< \dfrac{11}{19}\)
Do đó: \(\dfrac{26}{-37}< \dfrac{11}{19}\)
x: \(\dfrac{-7}{30}=\dfrac{-7\cdot2}{30\cdot2}=\dfrac{-14}{60}\)
\(\dfrac{13}{-20}=\dfrac{-13}{20}=\dfrac{-13\cdot3}{20\cdot3}=\dfrac{-39}{60}\)
mà -14>-39
nên \(-\dfrac{7}{30}< \dfrac{13}{-20}\)
y: \(-\dfrac{12}{16}=\dfrac{-12\cdot3}{16\cdot3}=\dfrac{-36}{48}\)
\(\dfrac{-16}{48}=\dfrac{-16}{48}\)
mà -36<-16
nên \(\dfrac{-12}{16}< -\dfrac{16}{48}\)
z: \(\dfrac{-18}{-72}=\dfrac{1}{4}>0\)
\(0>-\dfrac{5}{20}\)
Do đó: \(\dfrac{-18}{-72}>-\dfrac{5}{20}\)
z1: \(\dfrac{-36}{90}=\dfrac{-2}{5};\dfrac{-15}{25}=\dfrac{-3}{5}\)
mà -2>-3
nên \(\dfrac{-36}{90}>\dfrac{-15}{25}\)
z2: \(\dfrac{-32}{48}=\dfrac{-2}{3}=\dfrac{-4}{6}\)
\(\dfrac{-6}{12}=\dfrac{-1}{2}=\dfrac{-3}{6}\)
mà -4<-3
nên \(-\dfrac{32}{48}< -\dfrac{6}{12}\)
z3: \(\dfrac{-20}{-45}=\dfrac{4}{9}=\dfrac{40}{90}\)
\(\dfrac{35}{150}=\dfrac{7}{30}=\dfrac{21}{90}\)
mà 40>21
nên \(\dfrac{-20}{-45}>\dfrac{35}{150}\)

3:
\(6a+11b-6\left(a+7b\right)\)
\(=6a+11b-6a-42b=-31b⋮31\)
Ta có: \(\left(6a+11b\right)-6\left(a+7b\right)⋮31\)
\(6a+11b⋮31\)
Do đó: \(6\left(a+7b\right)⋮31\)
=>\(a+7b⋮31\)
Ta có: \(\left(6a+11b\right)-6\left(a+7b\right)⋮31\)
\(a+7b⋮31\)
Do đó: \(6a+11b⋮31\)
4:
\(5a+2b⋮17\)
=>\(12\left(5a+2b\right)⋮17\)
=>\(60a+24b⋮17\)
=>\(51a+17b+9a+7b⋮17\)
=>\(17\left(3a+b\right)+\left(9a+7b\right)⋮17\)
mà \(17\left(3a+b\right)⋮17\)
nên \(9a+7b⋮17\)

A = \(\dfrac{3n-13}{n-4}\) đkxđ n \(\ne\) 4
A \(\in\) Z ⇔ 3n - 13 \(⋮\) n - 4
3n - 12 - 1 \(⋮\) n - 4
(3n - 12) - 1 \(⋮\) n - 4
3.( n - 4) - 1 ⋮ n - 4
1 \(⋮\) n - 4
n - 4 \(\in\) Ư( 1) = { -1; 1}
n \(\in\) { 3; 5}
B = \(\dfrac{4n+19}{2n+3}\) (đkxđ n \(\ne\) - \(\dfrac{3}{2}\))
B = \(\dfrac{4n+19}{2n+3}\)
B \(\in\) Z ⇔ 4n + 19 \(⋮\) 2n + 3
4n + 6 + 13 ⋮ 2n + 3
13 ⋮ 2n + 3
2n + 3 \(\in\) Ư(13) = { -13; -1; 1; 13}
n \(\in\) { - 8; -2; -1; 5}
c, C = \(\dfrac{4n+35}{n-1}\) đkxđ n \(\ne\) 1
C \(\in\) Z ⇔ 4n + 35 ⋮ n - 1
4n - 4 + 39 ⋮ n - 1
4.(n-1) + 39 ⋮ n - 1
39 ⋮ n - 1
n - 1 \(\in\) Ư(39) = { -39; - 13; -3; -1; 1; 3; 13; 39}
n \(\in\) { - 38; -12; -2; 0; 2; 4; 14; 40}

=\(\frac{-13}{12}:\frac{-1}{12}-\frac{16}{15}\)\(:\frac{-2}{15}\)
=\(\frac{-13}{12}\times\left(\frac{-12}{1}\right)-\frac{16}{15}\times\frac{-15}{2}\)
=\(13-\left(-8\right)\)
=\(21\)
TÍCH ĐÚNG HỘ MÌNH VỚI Ạ
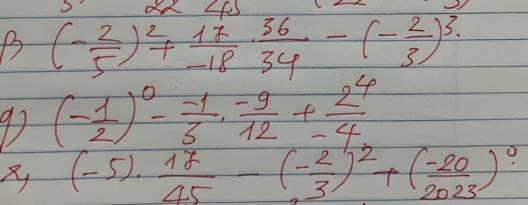
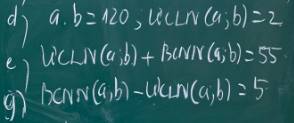

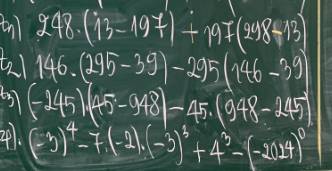
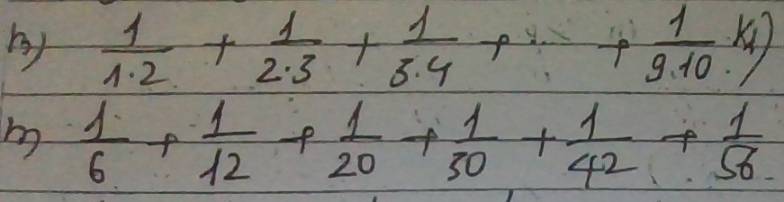 giúp em gấp phần m,n với ah cj ơi. Em cám ơn rấc nhìu ạa
giúp em gấp phần m,n với ah cj ơi. Em cám ơn rấc nhìu ạa

p: \(\left(-\dfrac{2}{5}\right)^2+\dfrac{17}{-18}\cdot\dfrac{36}{34}-\left(-\dfrac{2}{3}\right)^3\)
\(=\dfrac{4}{25}-\dfrac{17}{34}\cdot\dfrac{36}{18}-\dfrac{-8}{27}\)
\(=\dfrac{4}{25}+\dfrac{8}{27}-1=\dfrac{-367}{675}\)
q: \(\left(-\dfrac{1}{2}\right)^0-\dfrac{-1}{3}\cdot\dfrac{-9}{12}+\dfrac{2^4}{-4}\)
\(=1-\dfrac{1}{3}\cdot\dfrac{3}{4}+\dfrac{16}{-4}\)
\(=1-\dfrac{1}{4}-4=-3-\dfrac{1}{4}=-\dfrac{13}{4}\)
r: \(\left(-5\right)\cdot\dfrac{17}{45}-\left(-\dfrac{2}{3}\right)^2+\left(-\dfrac{20}{2023}\right)^0\)
\(=-\dfrac{17}{9}-\dfrac{4}{9}+1\)
\(=-\dfrac{21}{9}+1=-\dfrac{12}{9}=-\dfrac{4}{3}\)