
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


p: \(\dfrac{5}{1\cdot2}+\dfrac{5}{2\cdot3}+...+\dfrac{5}{50\cdot51}\)
\(=5\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{50\cdot51}\right)\)
\(=5\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{50}-\dfrac{1}{51}\right)\)
\(=5\cdot\left(1-\dfrac{1}{51}\right)=5\cdot\dfrac{50}{51}=\dfrac{250}{51}\)
q: \(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{1}{210}\)
\(=\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+...+\dfrac{2}{420}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{420}\right)\)
\(=2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{20\cdot21}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{20}-\dfrac{1}{21}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{21}\right)=2\cdot\dfrac{19}{42}=\dfrac{19}{21}\)

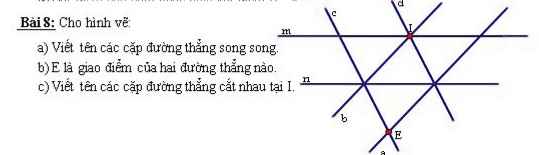
a: m//n
c//d
b//a
b:E là giao điểm của a và c
c: Các đường thẳng giao nhau tại I là d,m,b

Bài 3:
a) \(159-\left(25-x\right)=43\)
\(\Rightarrow25-x=159-43\)
\(\Rightarrow25-x=116\)
\(\Rightarrow x=25-116\)
\(\Rightarrow x=-91\)
b) \(\left(79-x\right)-43=-\left(17-52\right)\)
\(\Rightarrow\left(79-x\right)-43=-\left(-35\right)\)
\(\Rightarrow79-x=35+43\)
\(\Rightarrow79-x=78\)
\(\Rightarrow x=79-78\)
\(\Rightarrow x=1\)
c) \(-\left(-x+13-142\right)+18=55\)
\(\Rightarrow-\left(-x+13-142\right)=55-18\)
\(\Rightarrow x-13+142=37\)
\(\Rightarrow x+129=37\)
\(\Rightarrow x=37-129\)
\(\Rightarrow x=-92\)


bài 3:
tổng số giờ đã chảy đc từ 2 vòi : 1+1=2(giờ)
tổng số phần bể đã chảy được từ 2 vòi : \(\dfrac{1}{5}+\dfrac{1}{7}=\dfrac{7}{35}+\dfrac{5}{35}=\dfrac{12}{35}\left(ph\text{ần} b\text{ể}\right)\)
nếu chảy cùng lúc mỗi giờ chảy được : \(\dfrac{12}{35}:2=\dfrac{12}{35\cdot2}=\dfrac{6}{35}\left(ph\text{ần}b\text{ể}\right)\)
bài 4:
cách 1:
độ dài đoạn AB là : \(\dfrac{3}{4}+\dfrac{9}{8}=\dfrac{18}{24}+\dfrac{27}{24}=\dfrac{45}{24}\left(m\right)\)
diện tích ABCD là : \(\dfrac{45}{27}\cdot\dfrac{4}{7}=\dfrac{15}{14}\left(m^2\right)\)
cách 2:
diện tích AEFD là : \(\dfrac{3}{4}\cdot\dfrac{4}{7}=\dfrac{3}{7}\left(m^2\right)\)
diện tích EBCF là : \(\dfrac{9}{8}\cdot\dfrac{4}{7}=\dfrac{9}{14}\left(m^2\right)\)
diện tích ABCD là : \(\dfrac{3}{7}+\dfrac{9}{14}=\dfrac{15}{14}\left(m^2\right)\)

Số tiền Nam mua sách: \(320000\times\dfrac{1}{4}=80000\) (đồng)
Số tiền Nam mua vở: \(90000:\dfrac{2}{3}=135000\) (đồng)
Số tiền Nam mua dụng cụ học tập: \(320000-\left(80000+135000\right)=105000\) (đồng)


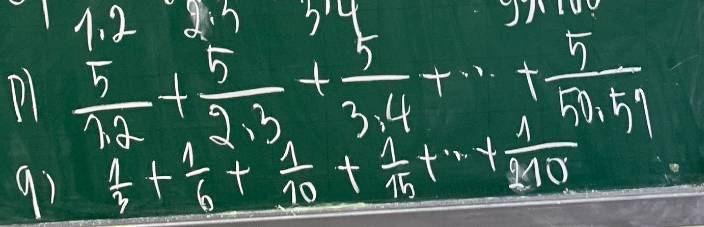



 Giúp em với ạ, em cần gấp trước 7h15 ạ. Em cảm ơn nhiều.
Giúp em với ạ, em cần gấp trước 7h15 ạ. Em cảm ơn nhiều.

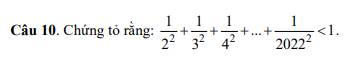
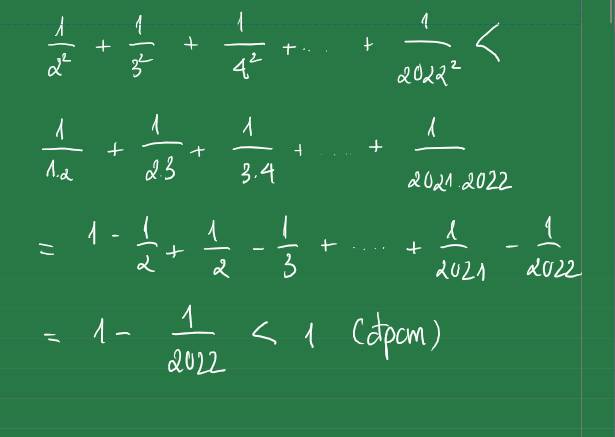
z4:
\(\dfrac{24}{148}=\dfrac{6}{37}=\dfrac{108}{37\cdot18}\)
\(\dfrac{-14}{-36}=\dfrac{7}{18}=\dfrac{7\cdot37}{18\cdot37}=\dfrac{259}{37\cdot18}\)
mà 108<259
nên \(\dfrac{24}{148}< \dfrac{-14}{-36}\)
z5: \(\dfrac{-26}{-72}=\dfrac{26}{72}< 1\)
\(1< \dfrac{45}{20}=\dfrac{-45}{-20}\)
Do đó: \(\dfrac{-26}{-72}< \dfrac{-45}{-20}\)
z6: \(\dfrac{14}{42}=\dfrac{1}{3}=\dfrac{1\cdot4}{3\cdot4}=\dfrac{4}{12}\)
\(\dfrac{21}{28}=\dfrac{3}{4}=\dfrac{3\cdot3}{4\cdot3}=\dfrac{9}{12}\)
mà 4<9
nên \(\dfrac{14}{42}< \dfrac{21}{28}\)
z7: \(\dfrac{-14}{-56}=\dfrac{1}{4}=\dfrac{5}{20}\)
\(\dfrac{21}{35}=\dfrac{3}{5}=\dfrac{3\cdot4}{5\cdot4}=\dfrac{12}{20}\)
mà 5<12
nên \(\dfrac{-14}{-56}< \dfrac{21}{35}\)
z8: \(10A=\dfrac{10^{201}+10}{10^{201}+1}=1+\dfrac{9}{10^{201}+1}\)
\(10B=\dfrac{10^{202}+10}{10^{202}+1}=1+\dfrac{9}{10^{202}+1}\)
\(10^{201}+1< 10^{202}+1\)
=>\(\dfrac{9}{10^{201}+1}>\dfrac{9}{10^{202}+1}\)
=>\(\dfrac{9}{10^{201}+1}+1>\dfrac{9}{10^{202}+1}+1\)
=>10A>10B
=>A>B