K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
15 tháng 12 2023
Câu II:
a) \(\sqrt{2x-1}=\sqrt{5}\left(x\ge\dfrac{1}{2}\right)\)
\(\Leftrightarrow2x-1=5\)
\(\Leftrightarrow2x=5+1\)
\(\Leftrightarrow2x=6\)
\(\Leftrightarrow x=\dfrac{6}{2}\)
\(\Leftrightarrow x=3\left(tm\right)\)
b) \(6\sqrt{x-5}+\sqrt{9x-45}-2\sqrt{4x-20}=25\left(x\ge5\right)\)
\(\Leftrightarrow6\sqrt{x-5}+\sqrt{9\left(x-5\right)}-2\sqrt{4\left(x-5\right)}=25\)
\(\Leftrightarrow6\sqrt{x-5}+3\sqrt{x-5}-2\cdot2\sqrt{x-5}=25\)
\(\Leftrightarrow9\sqrt{x-5}-4\sqrt{x-5}=25\)
\(\Leftrightarrow5\sqrt{x-5}=25\)
\(\Leftrightarrow\sqrt{x-5}=5\)
\(\Leftrightarrow x-5=5^2\)
\(\Leftrightarrow x-5=25\)
\(\Leftrightarrow x=30\left(tm\right)\)
15 tháng 12 2023
Bài III:
a:
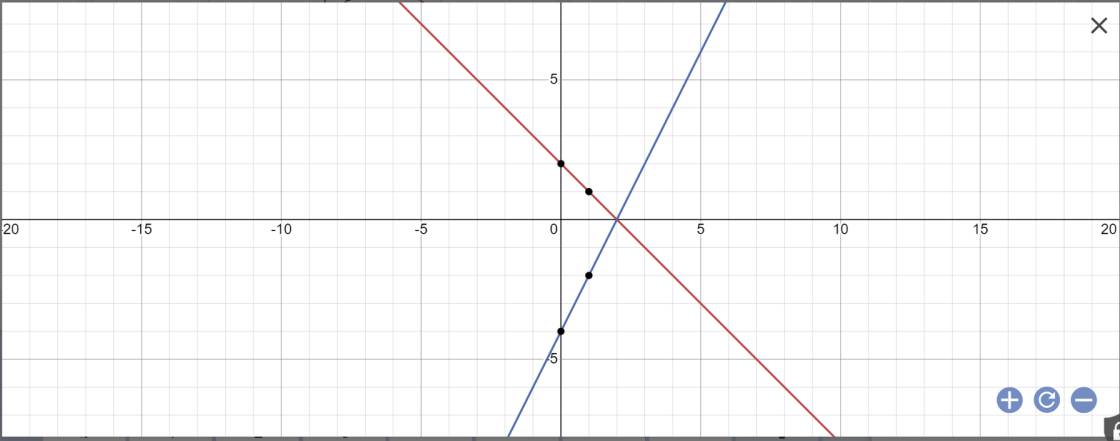
b: phương trình hoành độ giao điểm là:
2x-4=-x+2
=>2x+x=4+2
=>3x=6
=>x=6/3=2
Thay x=2 vào y=-x+2, ta được:
\(y=-2+2=0\)
Vậy: A(2;0)
c: Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-x+2=-0+2=2\end{matrix}\right.\)
Vậy: B(0;2)
Tọa độ C là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: C(0;-4)
Ta có: A(2;0); B(0;2); C(0;-4)
\(AB=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(0-2\right)^2+\left(-4-0\right)^2}=\sqrt{4^2+2^2}=2\sqrt{5}\)
\(BC=\sqrt{\left(0-0\right)^2+\left(-4-2\right)^2}=6\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{8+20-36}{2\cdot2\sqrt{2}\cdot2\sqrt{5}}=\dfrac{-8}{8\sqrt{5}}=-\dfrac{1}{\sqrt{5}}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\sqrt{1-\dfrac{1}{5}}=\dfrac{2}{\sqrt{5}}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{\sqrt{5}}\cdot2\sqrt{2}\cdot2\sqrt{5}=4\sqrt{2}\)
HK
1
12 tháng 12 2021
Đề 1:
Bài 1:
\(a,=\sqrt{\left(\sqrt{7}+1\right)^2}-\left|-1+\sqrt{7}\right|=\sqrt{7}+1-\sqrt{7}+1=2\\ b,=2\sqrt{2}-4\sqrt{2}-5\sqrt{2}+\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}-7\sqrt{2}=\dfrac{-13\sqrt{2}}{\sqrt{2}}\)
Bài 2:
\(PT\Leftrightarrow\sqrt{\left(x-\dfrac{1}{2}\right)^2}=\dfrac{1}{2}\Leftrightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}+\dfrac{1}{2}=1\\x=-\dfrac{1}{2}+\dfrac{1}{2}=0\end{matrix}\right.\)
Bài 3:
\(a,M=\dfrac{a-2\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{2\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)}=\dfrac{2}{\sqrt{a}+1}\\ b,M< 1\Leftrightarrow\dfrac{2}{\sqrt{a}+1}-1< 0\Leftrightarrow\dfrac{1-\sqrt{a}}{\sqrt{a}+1}< 0\\ \Leftrightarrow1-\sqrt{a}< 0\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a>1\)
AH
Akai Haruma
Giáo viên
28 tháng 5 2021
Bài 1:
a)
\(A=\left(\frac{4\sqrt{x}}{\sqrt{x}+2}-\frac{8x}{(\sqrt{x}-2)(\sqrt{x}+2)}\right):\left(\frac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-2)}-\frac{2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}\right)\)
\(=\frac{4\sqrt{x}(\sqrt{x}-2)-8x}{(\sqrt{x}-2)(\sqrt{x}+2)}:\frac{\sqrt{x}-1-2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}=\frac{-4x-8\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{-\sqrt{x}+3}\)
\(=\frac{-4\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{3-\sqrt{x}}=\frac{-4x(\sqrt{x}-2)}{(\sqrt{x}-2)(3-\sqrt{x})}=\frac{4x}{\sqrt{x}-3}\)
b)
Ta có:
\(m(\sqrt{x}-3).A>x+2025\)
\(\Leftrightarrow 4xm>x+2025\Leftrightarrow x(4m-1)>2025\)
\(\Leftrightarrow 4m-1>\frac{2025}{x}\Leftrightarrow m>\frac{1}{4}(\frac{2025}{x}+1)\) với mọi $x>9$
\(\Leftrightarrow m> \max \frac{1}{4}(\frac{2025}{x}+1), \forall x>9\Leftrightarrow m>56,5\)
mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
HM
0
28 tháng 10 2021
Câu 2:
a) ĐKXĐ: \(x\ge0\)
\(pt\Leftrightarrow\sqrt{3x}-10\sqrt{3x}+21\sqrt{3x}=12\)
\(\Leftrightarrow12\sqrt{3x}=12\Leftrightarrow\sqrt{3x}=1\Leftrightarrow3x=1\Leftrightarrow x=\dfrac{1}{3}\left(tm\right)\)
b) ĐKXĐ: \(x\ge2\)
\(pt\Leftrightarrow2\sqrt{x-2}-4\sqrt{x-2}=-1\)
\(\Leftrightarrow-2\sqrt{x-2}=-1\Leftrightarrow\sqrt{x-2}=\dfrac{1}{2}\)
\(\Leftrightarrow x-2=\dfrac{1}{4}\Leftrightarrow x=\dfrac{9}{4}\)
Câu 3:
\(A=\dfrac{5\sqrt{x}-25x}{1-5\sqrt{x}}=\dfrac{5\sqrt{x}\left(1-5\sqrt{x}\right)}{1-5\sqrt{x}}=5\sqrt{x}\)
14 tháng 12 2021
Câu 96: D. AB > CD (do AB là đường kính; CD là dây).
Câu 97: A. IC = ID (do CD \(\perp\) AB; CD là dây; AB là đường kính).
Bài 1:
a: \(\Leftrightarrow\left\{{}\begin{matrix}2x-4y=10\\3x+4y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{3}x+3y=\sqrt{3}\\2\sqrt{3}x+2y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\sqrt{3}\\x=1\end{matrix}\right.\)