K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
28 tháng 10 2021
2.
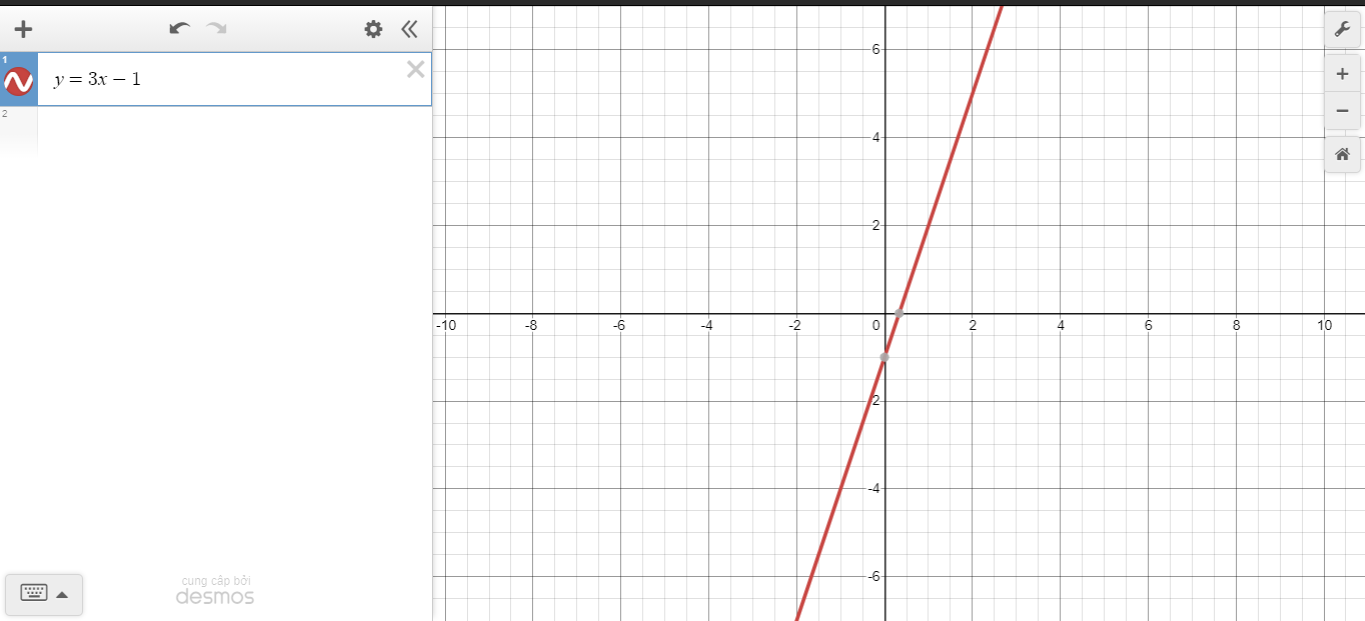
\(y=3x-1\) // \(y=3x-3\) vì \(\left\{{}\begin{matrix}3=3\\-1\ne-3\end{matrix}\right.\)
3.
\(a,y=\left(m+2\right)x-3//y=2x\Leftrightarrow\left\{{}\begin{matrix}m+2=2\\-3\ne0\end{matrix}\right.\Leftrightarrow m=0\)
\(b,\) Thay \(x=1;y=2\Leftrightarrow m+2-3=2\Leftrightarrow m=3\)
25 tháng 1 2022
Bài 1:
a: \(\Leftrightarrow\left\{{}\begin{matrix}2x-4y=10\\3x+4y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{3}x+3y=\sqrt{3}\\2\sqrt{3}x+2y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\sqrt{3}\\x=1\end{matrix}\right.\)
27 tháng 7 2021
Đặt \(A=\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\)
\(\Leftrightarrow A^3=2+\sqrt{5}+2-\sqrt{5}+3\cdot\sqrt[3]{\left(2+\sqrt{5}\right)\left(2-\sqrt{5}\right)}\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)\)
\(\Leftrightarrow A^3=4+3\cdot\left(-1\right)\cdot A\)
\(\Leftrightarrow A^3=4-3A\)
\(\Leftrightarrow A^3+3A-4=0\)
\(\Leftrightarrow A^3-A^2+A^2-A+4A-4=0\)
\(\Leftrightarrow A^2\left(A-1\right)+A\left(A-1\right)+4\left(A-1\right)=0\)
\(\Leftrightarrow\left(A-1\right)\left(A^2+A+4\right)=0\)
\(\Leftrightarrow A=1\)
20 tháng 9 2021
\(a,\) \(\left(d\right)\) đi qua \(A\left(1;2\right)\Leftrightarrow x=1;y=2\)
\(\Leftrightarrow2=m+1-2m+3\Leftrightarrow m=2\)
\(b,m=2\Leftrightarrow\left(d\right):y=3x-2\cdot2+3=3x-1\)
\(y=2\Leftrightarrow x=1\Leftrightarrow A\left(1;2\right)\\ y=5\Leftrightarrow x=2\Leftrightarrow B\left(2;5\right)\)
HT
2
BN
20 tháng 6 2016
bạn ơi giúp mình vs
tìm x,y, z nguyên thỏa mãn
x^3 + xyz = 957
y^3 + xyz = 759
z^3 + xyz = 579
TN
20 tháng 6 2016
\(\Leftrightarrow x-3\sqrt{x}-\sqrt{x-8}+1=0\)
\(\Leftrightarrow x=9\left(tm\right)\)
24 tháng 12 2021
1: Thay x=16 vào A, ta được:
\(A=\dfrac{16+3}{4-2}=\dfrac{19}{2}\)
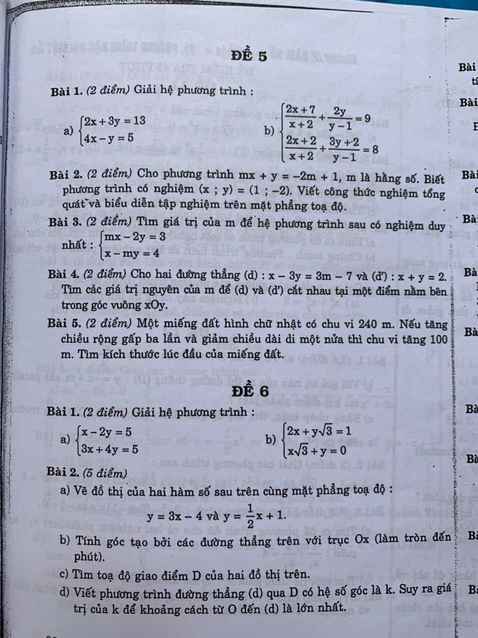
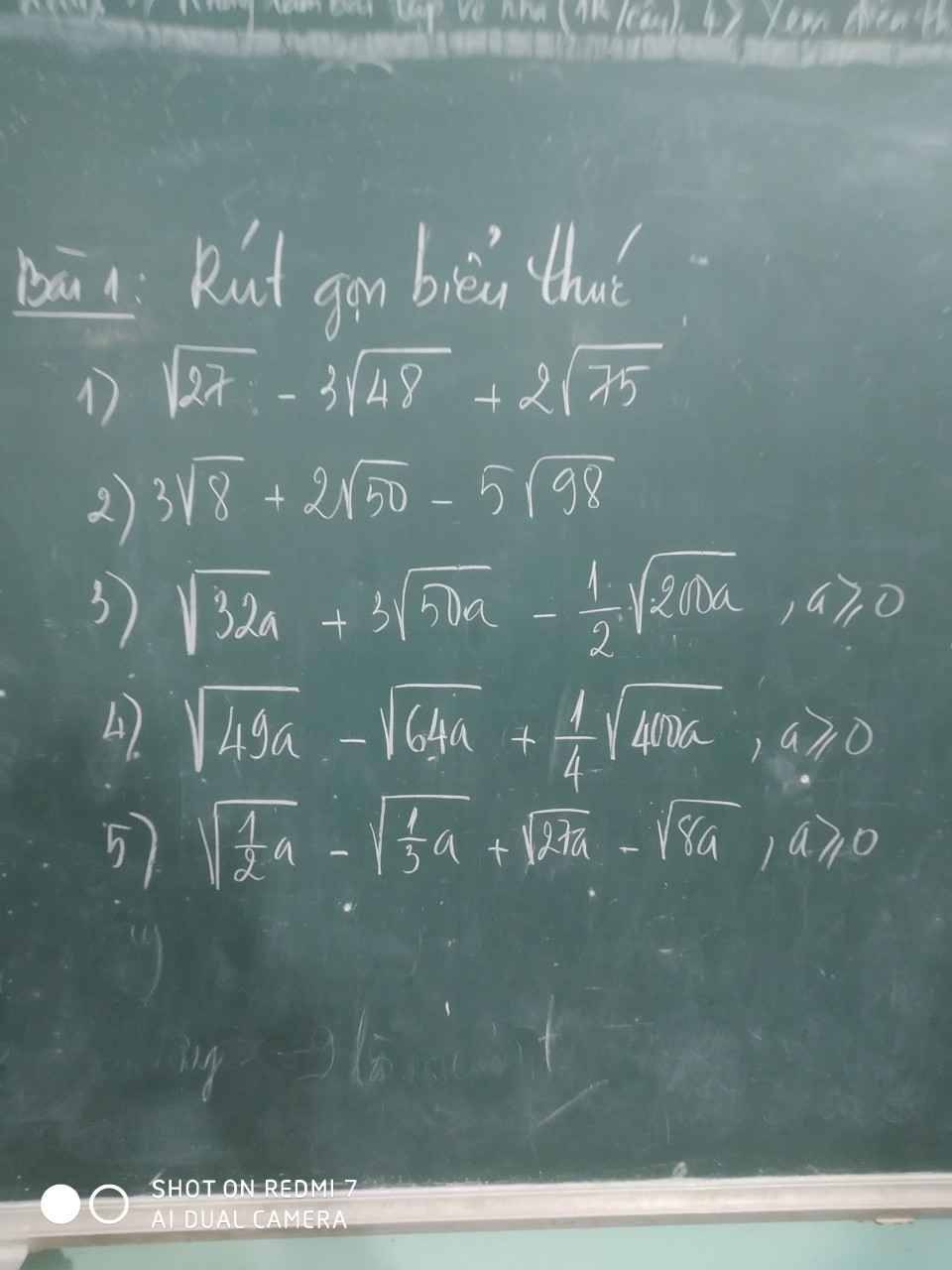
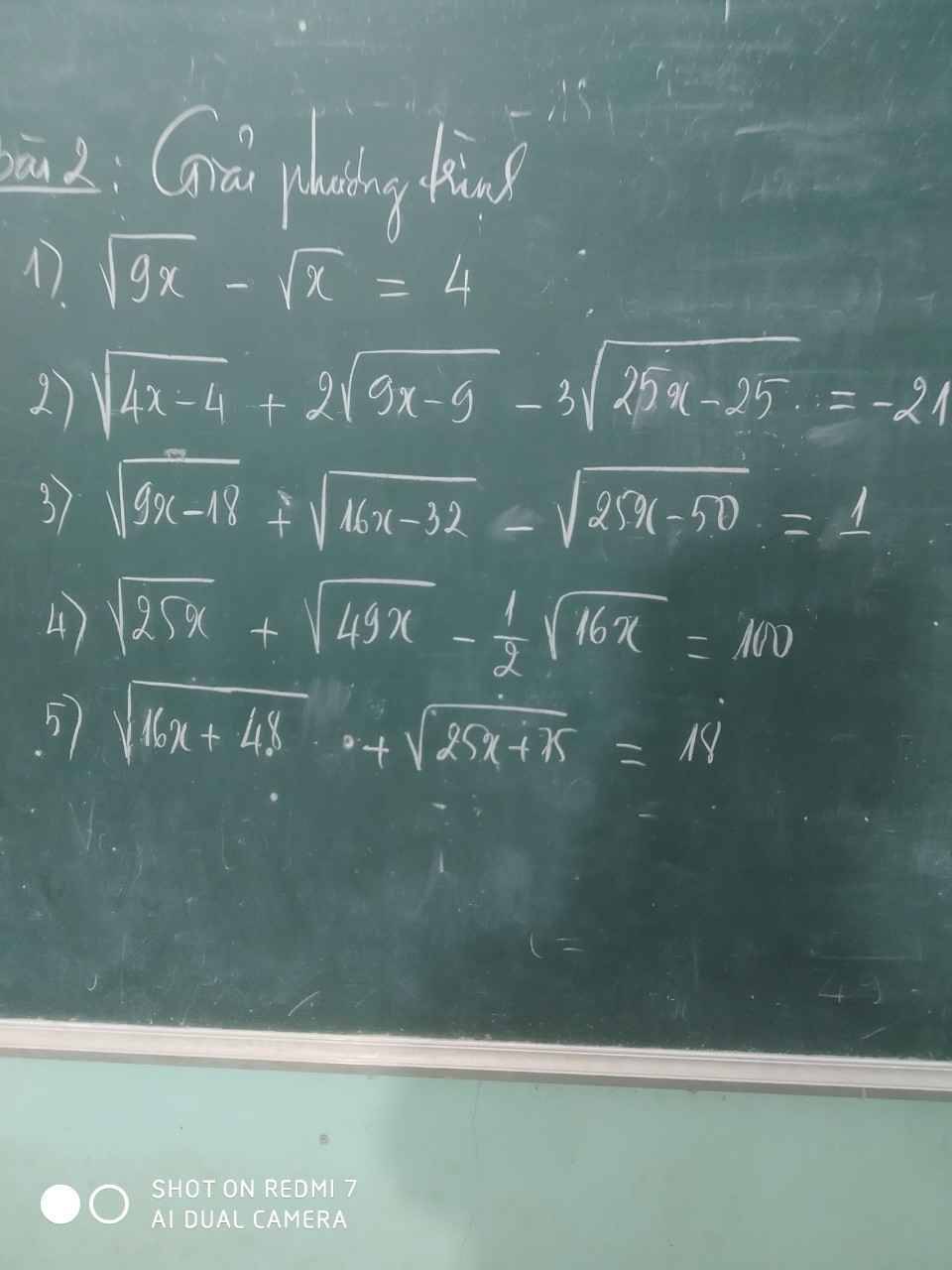
Câu 2:
a) ĐKXĐ: \(x\ge0\)
\(pt\Leftrightarrow\sqrt{3x}-10\sqrt{3x}+21\sqrt{3x}=12\)
\(\Leftrightarrow12\sqrt{3x}=12\Leftrightarrow\sqrt{3x}=1\Leftrightarrow3x=1\Leftrightarrow x=\dfrac{1}{3}\left(tm\right)\)
b) ĐKXĐ: \(x\ge2\)
\(pt\Leftrightarrow2\sqrt{x-2}-4\sqrt{x-2}=-1\)
\(\Leftrightarrow-2\sqrt{x-2}=-1\Leftrightarrow\sqrt{x-2}=\dfrac{1}{2}\)
\(\Leftrightarrow x-2=\dfrac{1}{4}\Leftrightarrow x=\dfrac{9}{4}\)
Câu 3:
\(A=\dfrac{5\sqrt{x}-25x}{1-5\sqrt{x}}=\dfrac{5\sqrt{x}\left(1-5\sqrt{x}\right)}{1-5\sqrt{x}}=5\sqrt{x}\)