Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của ô tô là x
=>Vận tốc xe máy là x-10
Theo đề, ta có: 120/(x-10)-120/x=1
=>(120x-120x+1200)/x(x-10)=1
=>x^2-10x=1200
=>x^2-10x-1200=0
=>x=40

\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}+\dfrac{1}{2-\sqrt{x}}\left(đk:x\ge0;x\ne4\right)\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-2}\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{3+2\sqrt{x}-4-\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{1}{\sqrt{x}+1}\)
\(S=\left(\dfrac{1}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\left(đk:x\ge0;x\ne1\right)\)
\(S=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\)
\(S=\dfrac{\sqrt{x}-2+x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{x+4\sqrt{x}+4}{1-\sqrt{x}}\)
\(S=\dfrac{x+3\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)
\(S=\dfrac{\left(x+3\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\left(1-\sqrt{x}\right)}\)
(đến đoạn này thì trong ngoặc ko tách ra đc nữa nên mik nghĩ là đến đây là xong, nếu sai thì bn nói mik)

a: \(=\dfrac{\sqrt{3}\left(x\sqrt{2}+y\sqrt{5}\right)}{2\left(x\sqrt{2}+y\sqrt{5}\right)}=\dfrac{\sqrt{3}}{2}\)
b: \(=\dfrac{a+\sqrt{a}-a-2}{\sqrt{a}+1}:\dfrac{a-\sqrt{a}+\sqrt{a}-4}{a-1}\)
\(=\dfrac{\left(\sqrt{a}-2\right)}{\sqrt{a}+1}\cdot\dfrac{a-1}{a-4}=\dfrac{\sqrt{a}-1}{\sqrt{a}+2}\)

a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2

a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp đường tròn đường kính AB
=>I là trung điểm của AB
b: Gọi H là giao của AD và BE
ABDE nội tiếp
=>góc HDE=góc HBA
=>góc HDE=góc HMN
=>DE//MN

a: góc AED+góc AFD=180 độ
=>AEDF nội tiếp
=>góc AEF=góc ADF=góc C
=>góc FEB+góc FCB=180 độ
=>FEBC nội tiếp
b: Xét ΔGBE và ΔGFC có
góc GBE=góc GFC
góc G chung
=>ΔGBE đồng dạng với ΔGFC
=>GB/GF=GE/GC
=>GB*GC=GF*GE

a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp


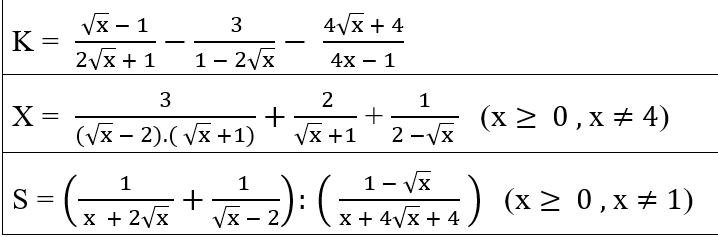
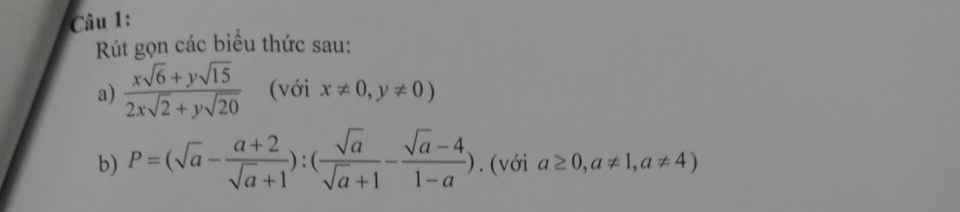





Đề 1:
Bài 1:
\(a,=\sqrt{\left(\sqrt{7}+1\right)^2}-\left|-1+\sqrt{7}\right|=\sqrt{7}+1-\sqrt{7}+1=2\\ b,=2\sqrt{2}-4\sqrt{2}-5\sqrt{2}+\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}-7\sqrt{2}=\dfrac{-13\sqrt{2}}{\sqrt{2}}\)
Bài 2:
\(PT\Leftrightarrow\sqrt{\left(x-\dfrac{1}{2}\right)^2}=\dfrac{1}{2}\Leftrightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}+\dfrac{1}{2}=1\\x=-\dfrac{1}{2}+\dfrac{1}{2}=0\end{matrix}\right.\)
Bài 3:
\(a,M=\dfrac{a-2\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{2\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)}=\dfrac{2}{\sqrt{a}+1}\\ b,M< 1\Leftrightarrow\dfrac{2}{\sqrt{a}+1}-1< 0\Leftrightarrow\dfrac{1-\sqrt{a}}{\sqrt{a}+1}< 0\\ \Leftrightarrow1-\sqrt{a}< 0\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a>1\)