Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có : \(2sin^2x+3cos2x=0\Leftrightarrow2sin^2x+3\left(1-2sin^2x\right)=0\)
\(\Leftrightarrow3-4sin^2x=0\Leftrightarrow sin^2x=\dfrac{3}{4}\Leftrightarrow sinx=\pm\dfrac{\sqrt{3}}{2}\)
th1 : \(sinx=\dfrac{\sqrt{3}}{2}\Leftrightarrow sinx=sin\dfrac{\pi}{3}\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)th2 : \(sinx=\dfrac{-\sqrt{3}}{2}\Leftrightarrow sinx=sin\left(\dfrac{-\pi}{3}\right)\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-\pi}{3}+k2\pi\\x=\pi+\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-\pi}{3}+k2\pi\\x=\dfrac{4\pi}{3}+k2\pi\end{matrix}\right.\)
vậy phương trình có 4 hệ nghiệm : \(x=\dfrac{\pi}{3}+k2\pi;x=\dfrac{2\pi}{3}+k2\pi;x=\dfrac{-\pi}{3}+k2\pi;x=\dfrac{4\pi}{3}+k2\pi\)

a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)

3 cos 2 x - 2 sin 2 x + sin 2 x = 1
Với cosx = 0 ta thấy hai vế đều bằng 1. Vậy phương trình có nghiệm x = 0,5π + kπ, k ∈ Z
Trường hợp cosx ≠ 0, chia hai vế cho cos2x ta được:
3 - 4 tan x + tan 2 x = 1 + tan 2 x ⇔ 4 tan x = 2 ⇔ tan x = 0 , 5 ⇔ x = a r c tan 0 , 5 + k π , k ∈ Z
Vậy nghiệm của phương trình là
x = 0,5π + kπ, k ∈ Z
và x = arctan 0,5 + kπ, k ∈ Z

a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5). c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2 ⇔ d) 5cos2x + 12sin2x -13 = 0 ⇔ Đặt α = arccos5/13 thì phương trình trở thành cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1 ⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).

a. cos2x = 1-sin2x
b. cos2x = 2cos2x - 1
c. 2cosx.cos2x = 1 + cos2x + cos3x
=> 2cosx.cos2x = 2cos2x + 4cos3x - 3cosx
=> cosx(2.(2cos2x - 1) - 2cosx - 4cos2x +3) = 0
=> cosx( -2cosx + 1) = 0
=> cosx=0 hoặc cosx = -1/2

\(\left(2cosx+1\right)\left(3cos2x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\3cos2x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\cos2x=\dfrac{4}{3}>1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\dfrac{2\pi}{3}+k2\pi\)

Hướng dẫn giải:
Chọn A.
![]() không là nghiệm của phương trình
không là nghiệm của phương trình
Chia 2 vế phương trình cho cos2x ta được
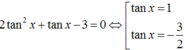
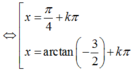
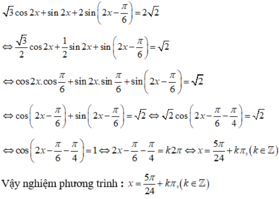
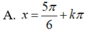
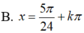
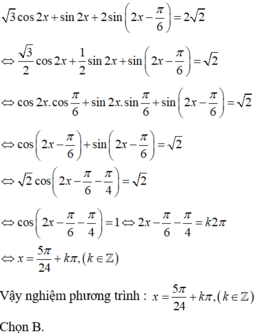
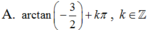
a) ta có : \(2sin^2x+3cos2x=0\Leftrightarrow2sin^2x+3\left(1-2sin^2x\right)=0\)
\(\Leftrightarrow3-4sin^2x=0\Leftrightarrow sin^2x=\dfrac{3}{4}\Leftrightarrow sinx=\pm\dfrac{\sqrt{3}}{2}\)
th1 : \(sinx=\dfrac{\sqrt{3}}{2}\Leftrightarrow sinx=sin\dfrac{\pi}{3}\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)th2 : \(sinx=\dfrac{-\sqrt{3}}{2}\Leftrightarrow sinx=sin\left(\dfrac{-\pi}{3}\right)\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-\pi}{3}+k2\pi\\x=\pi+\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-\pi}{3}+k2\pi\\x=\dfrac{4\pi}{3}+k2\pi\end{matrix}\right.\)
vậy phương trình có 4 hệ nghiệm : \(x=\dfrac{\pi}{3}+k2\pi;x=\dfrac{2\pi}{3}+k2\pi;x=\dfrac{-\pi}{3}+k2\pi;x=\dfrac{4\pi}{3}+k2\pi\)
câu b bn làm tương tự cho quen nha