
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3cos2x - 5 cos x + 2 = 0
Đặt cos x = t với điều kiện -1 ≤ t ≤ 1 (*),
ta được phương trình bậc hai theo t:
3t2 - 5t + 2 = 0(1)
Δ = (-5)2 - 4.3.2 = 1
Phương trình (1)có hai nghiệm là:
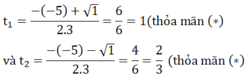
Ta có:
cosx = 1 ⇔ cosx = cos0
⇔ x = k2π, k ∈ Z
cosx = 2/3 ⇔ x = ± arccos 2/3 + k2π, k ∈ Z

3 cos 2 x - 2 sin x + 2 = 0 ⇔ 3 ( 1 - sin 2 x ) - 2 sin x + 2 = 0 ⇔ 3 sin 2 x + 2 sin x - 5 = 0 ⇔ ( sin x - 1 ) ( 3 sin x + 5 ) = 0 ⇔ sin x = 1 ⇔ x = π / 2 + k 2 π , k ∈ Z

1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)


3 cos 2 x - 2 sin 2 x + sin 2 x = 1
Với cosx = 0 ta thấy hai vế đều bằng 1. Vậy phương trình có nghiệm x = 0,5π + kπ, k ∈ Z
Trường hợp cosx ≠ 0, chia hai vế cho cos2x ta được:
3 - 4 tan x + tan 2 x = 1 + tan 2 x ⇔ 4 tan x = 2 ⇔ tan x = 0 , 5 ⇔ x = a r c tan 0 , 5 + k π , k ∈ Z
Vậy nghiệm của phương trình là
x = 0,5π + kπ, k ∈ Z
và x = arctan 0,5 + kπ, k ∈ Z

Chọn D.
Trước tiên, ta có: y’ = 2cos2x + 2sinx.
Khi đó, phương trình có dạng:
2cos2x + 2sinx = 0 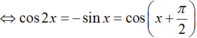

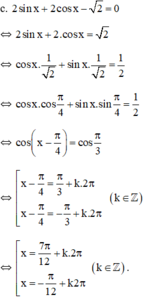
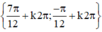 (k ∈ Z)
(k ∈ Z)
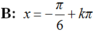
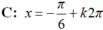


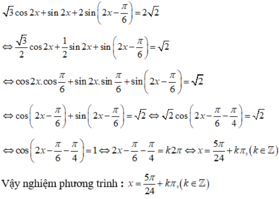
\(\left(2cosx+1\right)\left(3cos2x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\3cos2x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\cos2x=\dfrac{4}{3}>1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\dfrac{2\pi}{3}+k2\pi\)
Tương đương cosx = cos1200