K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2020
Đặt \(T=\left|\sqrt{4x^2-12x+10}-\sqrt{4x^2+20x+74}\right|\)
\(T=\left|\sqrt{\left(2x-3\right)^2+1}-\sqrt{\left(2x+5\right)^2+7^2}\right|\)
Trong hệ tọa độ Oxy, xét \(M\left(2x;0\right);A\left(3;1\right);B\left(-5;7\right)\)
Ta có: \(\left\{{}\begin{matrix}AM=\sqrt{\left(2x-3\right)^2+1}\\BM=\sqrt{\left(2x+5\right)^2+7^2}\end{matrix}\right.\) ; \(AB=\sqrt{8^2+6^2}=10\)
\(\Rightarrow T=\left|AM-BM\right|\le AB=10\)
\(\Rightarrow0\le T\le10\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(0\le m\le10\)
Có 11 giá trị nguyên của m thỏa mãn
ND
1
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2021
\(\Leftrightarrow7x-7=16-4y\)
\(\Leftrightarrow7\left(x-1\right)=4\left(4-y\right)\)
Do 7 và 4 nguyên tố cùng nhau
\(\Rightarrow x-1⋮4\Rightarrow x-1=4k\Rightarrow x=4k+1\)
\(\Rightarrow y=-7k+4\)
Vậy nghiệm của pt có dạng: \(\left(x;y\right)=\left(4k+1;-7k+4\right)\) với \(k\in Z\)
CM
30 tháng 3 2019
Chọn C.
Ta có:
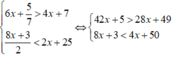
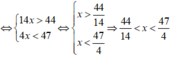
Mà x nguyên ⇒ x ∈ {4;5;....;11}
Vậy có 8 giá trị của x thỏa mãn hệ bất phương trình.
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2021
Đường tròn (C) tâm \(I\left(2;4\right)\) bán kính \(R=5\)
Điểm A thuộc (C) nên tiếp tuyến d qua A vuông góc IA
\(\Rightarrow\overrightarrow{AI}=\left(3;4\right)\Rightarrow\) đường thẳng d nhận (3;4) là 1 vtpt
Phương trình d:
\(3\left(x+1\right)+4\left(y-0\right)=0\Leftrightarrow3x+4y+3=0\)
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
3 tháng 1 2021
Đặt \(\sqrt{\dfrac{4x+9}{28}}=y+\dfrac{1}{2}\left(y\ge-\dfrac{1}{2}\right)\).
Ta có hpt:
\(\left\{{}\begin{matrix}14y^2+14y=2x+1\\14x^2+14x=2y+1\end{matrix}\right.\)
\(\Rightarrow14\left(x^2-y^2\right)+16\left(x-y\right)=0\Leftrightarrow\left[{}\begin{matrix}x-y=0\\x+y=\dfrac{-8}{7}\end{matrix}\right.\).
Đến đây thế vào là được.
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 1 2022
ĐKXĐ: \(x\ge0\)
- Với \(x=0\) không phải nghiệm
- Với \(x>0\) , chia 2 vế của pt cho \(x\) ta được:
\(\dfrac{4x^2+1}{x}+2\sqrt{\dfrac{4x^2+1}{x}}+3-2m=0\)
Đặt \(t=\sqrt{\dfrac{4x^2+1}{x}}\ge\sqrt{\dfrac{2\sqrt{4x^2}}{x}}=2\)
Pt trở thành: \(t^2+2t+3-2m=0\)
\(\Leftrightarrow t^2+2t+3=2m\) (1)
Pt đã cho có nghiệm khi và chỉ khi (1) có nghiệm \(t\ge2\)
Xét hàm \(f\left(t\right)=t^2+2t+3\) khi \(t\ge2\)
Do \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=-1< 2\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge2\)
\(\Rightarrow f\left(t\right)\ge f\left(2\right)=11\)
\(\Rightarrow\) Pt có nghiệm khi \(2m\ge11\Rightarrow m\ge\dfrac{11}{2}\)
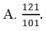
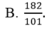
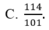
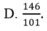
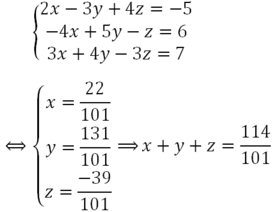
tớ phân tích được:
(4-5y)(5x-4)=-66
nhưng không biết nhận xét để rút bớt nghiệm mong các cậu giúp đỡ
À nếu có cách khác thì chỉ tớ với nhé