
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vẽ đồ thị:
- Vẽ đồ thị hàm số y = f(x) = x + 1 qua hai điểm (0; 1) và (-1; 0).
- Vẽ đồ thị hàm số y = g(x) = 3 - x qua hai điểm (0; 3) và (3; 0)
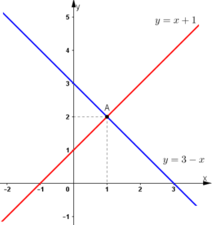
a) Nghiệm của phương trình f(x) = g(x) chính là hoành độ giao điểm của hai đường thẳng y = f(x) và y = g(x).
Giao điểm của hai đường thẳng y = x + 1 và y = 3 – x là điểm A(1; 2).
Do đó phương trình f(x) = g(x) có nghiệm x = 1.
Kiểm tra bằng tính toán:
f(x) = g(x) ⇔ x + 1 = 3 - x ⇔ 2x = 2 ⇔ x = 1.
b) Khi x > 1 thì đồ thị hàm số y = f(x) nằm phía trên đồ thị hàm số y = g(x), hay với x > 1 thì f(x) > g(x).
Kiểm tra bằng tính toán:
f(x) > g(x) ⇔ x + 1 > 3 - x ⇔ 2x > 2 ⇔ x > 1.
c) Khi x < 1 thì đồ thị hàm số y = f(x) nằm phía dưới đồ thị hàm số y = g(x), hay với x < 1 thì f(x) < g(x).
Kiểm tra bằng tính toán:
f(x) < g(x) ⇔ x + 1 < 3 - x ⇔ 2x < 2 ⇔ x < 1.

Lời giải
$y'=3x^2+1>0$ với mọi $x\in\mathbb{R}$ nên hàm $y=x^3+x$ đồng biến trên $\mathbb{R}$
PT $\Leftrightarrow x^3+x=\sqrt[3]{2x+1}+2x+1$
Đặt $\sqrt[3]{2x+1}=t$ thì:
$x^3+x=t^3+t$
Vì hàm $y=x^3+x$ đồng biến nên $x^3+x=t^3+t\Leftrightarrow x=t$
$\Leftrightarrow x=\sqrt[3]{2x+1}$
$\Leftrightarrow x^3=2x+1$
Giải pt này dễ dàng có $x=-1; \frac{1\pm \sqrt{5}}{2}$

HPT ⇔\(\begin{cases}+z_2=2+3\iota\\z_1.z_2=-5+8\iota\end{cases}\)
z1 và z2 là 2 nghiệm phương trình :
z2-(2+3\(\iota\) )z -5+8\(\iota\) =0
ta có:
\(\Delta\) =15-20\(\iota\) =[\(\sqrt{5}\left(2-\iota\right)\)]2
nên \(\left[\begin{array}{nghiempt}=\left(1+\sqrt{5}\right)+\frac{3-\sqrt{5}}{2}\iota\\z_2=\left(1-\sqrt{5}\right)+\frac{3+\sqrt{5}}{2}\iota\end{array}\right.\)

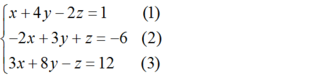
Đưa hệ phương trình về dạng hệ tam giác bằng cách khử dần các ẩn.
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và cộng phương trình (2) với phương trình (3) ta được:
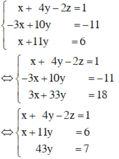
Giải hệ phương trình trên ta được
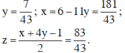
Vậy hệ phương trình có nghiệm 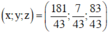

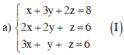
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số ta có:
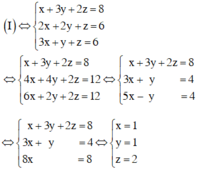
Vậy hệ phương trình có nghiệm (x; y; z) = (1; 1; 2).

a) Quan sát vào độ thị ta thấy đoạn mà đồ thị nằm dưới truch hoành là \(\left[ { - 2;\frac{5}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} - 0,5x - 5 \le 0\) là đoạn \(\left[ { - 2;\frac{5}{2}} \right]\)
b) Quan sát vào đồ thị ta thấy đồ thị luôn nằm dưới trục hoành
Vậy nghiệm của bất phương trình \( - 2{x^2} + x - 1 > 0\) vô nghiệm


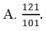
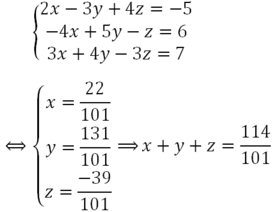
không đọc được