Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(p=x+y+z\)
\(q=xy+zy+zx\)
\(r=xyz\)
Ta có :
\(2q=\left(x+y+z\right)^2-\left(x^2+y^2+z^2\right)=4-6=-2\Rightarrow q=-1\)
Bây giờ ta sẽ đi tìm r
Đặt \(S_n=x^n+y^n+z^n\)
Khi đó \(S_0=3\)
\(S_1=-2\)
\(S_2=6\)
Ta có :
\(S_n-\left(x+y+z\right)S_{n-1}+\left(xy+yz+zx\right)S_{n-2}-xýzS_{n-3}=0\)
Suy ra \(S_n=-2S_{n-1}+S_{n-2}+rS_{n-3}\)
Lấy n = 3, ta được :
\(S_3=-2S_2+S_1+rS_0=-14+3r\)
Lấy n = 4, ta được :
\(S_4=-2S_3+S_2+rS_1=28-6r+6-2r=34-8r\)
Lấy n = 5, ta được :
\(S_5=-2S_4+S_3+rS_2=-68+16r-14+3r+6r=-82+25r\)
Mà \(S_5=-32\) nên r = 2.
Do đó x, y, z là nghiệm của phương trình
\(t^3+2t^2-t-2=0\Leftrightarrow t\in\left\{1;-1;-2\right\}\)
Vậy nghiệm của hệ là \(\left\{1;-1;-2\right\}\) và các hoán vị của nó

3 an 2 phuong trinh cai nay toan Dai Hoc ma

\(\frac{27}{3\sqrt{3x-2}+6}+\frac{8+4x-x^2}{x\sqrt{6-x}+4}\ge\frac{3}{2}+\frac{2x-14}{3\sqrt{6-x}+2}>0\)
Nên phần còn lại vô nghiệm

\(\left\{{}\begin{matrix}\left(x+1\right)\left(x^2+1\right)=y^3+1\\\left(y+1\right)\left(y^2+1\right)=z^3+1\\\left(z+1\right)\left(z^2+1\right)=x^3+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^3+x^2+x=y^3\left(1\right)\\y^3+y^2+y=z^3\\z^3+z^2+z=x^3\end{matrix}\right.\)
Giả sử \(x>y\Rightarrow x^3+x^2+x>y^3+y^2+y\)
\(\Rightarrow y^3>z^3\Leftrightarrow y>z\left(2\right)\)
\(\Rightarrow y^3+y^2+y>z^3+z^2+z\Rightarrow z>x\left(3\right)\)
Từ \(\left(2\right);\left(3\right)\Rightarrow y>x\) (Vô lí)
Giả sử \(x< y\Rightarrow x^3+x^2+x< y^3+y^2+y\)
\(\Rightarrow y^3< z^3\Leftrightarrow y< z\left(4\right)\)
\(\Rightarrow y^3+y^2+y< z^3+z^2+z\Rightarrow z< x\left(5\right)\)
Từ \(\left(4\right);\left(5\right)\Rightarrow y< x\) (Vô lí)
\(\Rightarrow x=y=z\)
\(\left(1\right)\Leftrightarrow x^3+x^2+x=x^3\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow x=y=z=0\) hoặc \(x=y=z=-1\)

ĐKXĐ : \(2\le x,y,z\le4\)
Từ hệ phương trình ta suy ra được
\(\Sigma x+\Sigma\sqrt{x-2}+\Sigma\sqrt{4-x}=\Sigma x^2-5\Sigma x+33\\ \Leftrightarrow\Sigma\left(x^2-6x+9\right)+6=\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\\ \Leftrightarrow\Sigma\left(x-3\right)^2+6=\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\left(1\right)\)
Áp dụng bất đẳng thức \(\sqrt{A}+\sqrt{B}\le\sqrt{2\left(A+B\right)}\)
\(\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\le\Sigma\sqrt{2\left(x-2+4-x\right)}=\Sigma2=6\)
\(\Rightarrow\Sigma\left(x-3\right)^2+6\le6\Rightarrow\Sigma\left(x-3\right)^2\le0\)
Mà \(\Sigma\left(x-3\right)^2\ge0\)
\(\Rightarrow\left(x-3\right)^2=\left(y-3\right)^2=\left(z-3\right)^2=0\\ \Leftrightarrow x=y=z=3\)
Thay vào ta thấy thỏa mãn -> x=y=z=3 là nghiệm hpt

a) \(\left\{{}\begin{matrix}x+3y+2z=8\\2x+2y+z=6\\3x+y+z=6\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\\z=2\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x-3y+2z=-7\\-2x+4y+3z=8\\3x+y-z=5\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{11}{14}\\y=\dfrac{5}{2}\\z=-\dfrac{1}{7}\end{matrix}\right.\)
a) Đặt \(\left\{{}\begin{matrix}x+3y+2z=8\left(1\right)\\2x+2y+z=6\left(2\right)\\3x+y+z=6\left(3\right)\end{matrix}\right.\)
Cộng \(\left(2\right)+\left(3\right)\) ta có:\(\left\{{}\begin{matrix}x+3y+2z=8\left(1\right)\\2x+2y+z=6\left(2\right)\\5x+3y+2z=12\left(4\right)\end{matrix}\right.\)
Trừ \(\left(4\right)-\left(1\right)\) ta được: \(4x=4\Leftrightarrow x=1\).
Thay vào hệ phương trình ta được:
\(\left\{{}\begin{matrix}1+3y+2z=8\\2.1+2y+z=6\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\z=2\end{matrix}\right.\).
Vậy hệ phương trình có nghiệm: \(\left\{{}\begin{matrix}x=1\\y=1\\z=2\end{matrix}\right.\).
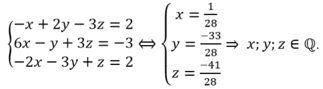
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số ta có:
Vậy hệ phương trình có nghiệm (x; y; z) = (1; 1; 2).