K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TB
26 tháng 10 2021
\(4\sin^22x-4\cos2x-1=0\)
\(\Leftrightarrow4\left(1-\cos^22x\right)-4\cos2x-1=0\)
\(\Leftrightarrow4-4\cos^22x-4\cos2x-1=0\)
\(\Leftrightarrow-4\cos^22x-4\cos2x+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\cos2x=\dfrac{-3}{2}\left(L\right)\end{matrix}\right.\Leftrightarrow\cos2x=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}-k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}-k\pi\end{matrix}\right.\left(k\in Z\right)\)
Chọn A
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 12 2021
Mỗi câu hỏi có \(\dfrac{1}{4}\) khả năng trả lời đúng và \(\dfrac{3}{4}\) khả năng trả lời sai
Có 3 trường hợp thỏa mãn: học sinh trả lời đúng 7 câu, 8 câu, 9 câu
Xác suất:
\(P=C_9^7.\left(\dfrac{1}{4}\right)^7.\left(\dfrac{3}{4}\right)^2+C_9^8.\left(\dfrac{1}{4}\right)^8.\left(\dfrac{3}{4}\right)^1+C_9^9.\left(\dfrac{1}{4}\right)^9=\dfrac{11}{8192}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
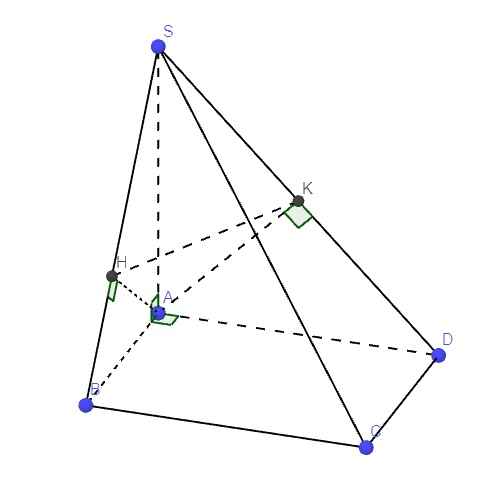
\(SA\perp\left(ABCD\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AB\\SA\perp AD\end{matrix}\right.\) \(\Rightarrow\) các tam giác SAB và SAD vuông tại A
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\Delta SBC\) vuông tại B
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\Rightarrow\Delta SCD\) vuông tại D
b.
\(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\Rightarrow BC\perp AH\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (1)
\(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp AK\\AK\perp SD\end{matrix}\right.\) \(\Rightarrow AK\perp\left(SCD\right)\Rightarrow AK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(AHK\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)
1 tháng 11 2023
Để giải thích câu trắc nghiệm này, ta cần xem xét vị trí của các điểm M, M', N, N' trên cạnh AB và CD của tứ diện ABCD. Nếu các điểm M, M', N, N' được chọn sao cho MN và M'N' là hai đường thẳng song song, tức là MN // M'N', thì đáp án là D. song song. Nếu các điểm M, M', N, N' được chọn sao cho MN và M'N' là hai đường thẳng chéo nhau, tức là MN và M'N' cắt nhau tại một điểm, thì đáp án là C. chéo nhau.
Tuy nhiên, câu trắc nghiệm không đưa ra thông tin cụ thể về vị trí của các điểm M, M', N, N', nên không thể xác định chính xác đáp án. Do đó, đáp án có thể là B. cắt nhau hoặc song song.
Vì vậy, câu trả lời cuối cùng là B. cắt nhau hoặc song song.
a: y'=4x^2+2x-m
Δ=2^2-4*4*(-m)=16m+4
y'>=0 với mọi x thì 16m+4<=0
=>m<=-1/4
b: x=1 =>y=2+1-m+5=-m+8 và y'=4+2-m=-m+6
y-f'(1)=f(1)(x-1)
=>y=(-m+8)(x-1)-m+6
=x(-m+8)+m-8-m+6
=x(-m+8)-2
Tọa độ A là: x=0 và y=-2
Tọa độ B là: y=0 và x=2/(-m+8)
=>OA=2; OB=2/|m-8|
Theo đề, ta có: |m-8|=1
=>m=9 hoặc m=7