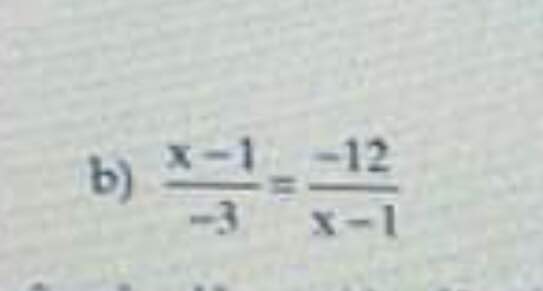K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 12 2020
a) Xét ΔADB và ΔADC có
AB=AC(gt)
AD chung
DB=DC(D là trung điểm của BC)
Do đó: ΔADB=ΔADC(c-c-c)
b) Ta có: AB=AC(gt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DB=DC(D là trung điểm của BC)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AD là đường trung trực của BC
hay AD⊥BC(đpcm)
c) Ta có: CE⊥BC(gt)
AD⊥BC(cmt)
Do đó: EC//AD(Định lí 1 từ vuông góc tới song song)
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
15 tháng 4 2022
a: Xét ΔAMB và ΔANC có
AM=AN
\(\widehat{BAM}\) chung
AB=AC
Do đó: ΔAMB=ΔANC
Xét ΔBNC và ΔCMB có
NB=MC
BC chung
NC=MB
Do đó: ΔBNC=ΔCMB
b: Ta có: ΔABM=ΔACN
nên BM=CN
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)
nên ΔGBC cân tại G
Xét ΔABG và ΔACG có
AB=AC
BG=CG
AG chung
Do đó: ΔABG=ΔACG
Suy ra: \(\widehat{BAG}=\widehat{CAG}\)
hay AG là tia phân giác của góc BAC
HL
3
LD
10 tháng 11 2021
\(=4\)
Cái này thì bạn rút gọn x - 1 thì còn \(\dfrac{-12}{-3}\)
Sau đó rút gọn -12 và -3 thì chỉ còn 4 thôi
10 tháng 11 2021
=>(x-1)2 = -12 . (-3)
(x-1)2 = 36
(x-1)2 = 62 = (-6)2
*) x-1=6 *) x-1=-6
x=7 x=-5
=>x thuộc (7,-5)
11 tháng 7 2023
1: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AB//CD và AB=CD
2: Xét ΔBAE có
BM,AE là trung tuyến
BM cắt AE tại I
=>I là trọng tâm
=>MI=1/3MB
Xét ΔCAD có
DF,CM là trung tuyến
DF cắt CM tại K
=>K là trọng tâm
=>MK=1/3MC
=>MI=MK
17 tháng 11 2016
Xét 3 trường hợp:
- TH1: x < 12,2 ta có: (12,2 - x) + (22,6 - x) = 10
=> 34,8 - 2x = 10
=> 2x = 34,8 - 10 = 24,8
=> x = 24,8 : 2 = 12,4; không thỏa mãn x < 12,2
- TH2: \(12,2\le x< 22,6\) ta có: (x - 12,2) + (22,6 - x) = 10
=> 10,4 = 10; vô lý
- TH3: x \(\ge\) 22,6 ta có: (x - 12,2) + (x - 22,6) = 10
=> 2x - 34,8 = 10
=> 2x = 10 + 34,8 = 44,8
=> x = 44,8 : 2 = 22,4; không thỏa mãn x \(\ge\) 22,6
Vậy số giá trị của x thỏa mãn là 0
1 tháng 8 2016
Theo đầu bài ta có:
\(\frac{x+1}{2}=\frac{y+3}{4}=\frac{z+5}{6}\)
\(\Rightarrow\frac{2\cdot\left(x+1\right)}{2\cdot2}=\frac{3\cdot\left(y+3\right)}{3\cdot4}=\frac{4\cdot\left(z+5\right)}{4\cdot6}\)
\(\Rightarrow\frac{2x+2}{4}=\frac{3y+9}{12}=\frac{4z+20}{24}\)
\(=\frac{\left(2x+2\right)+\left(3y+9\right)+\left(4z+20\right)}{4+12+24}\)
\(=\frac{\left(2x+3y+4z\right)+\left(2+9+20\right)}{4+12+24}\)
\(=\frac{9+31}{40}=1\)
\(\Rightarrow\hept{\begin{cases}x=1\cdot2-1=1\\y=1\cdot4-3=1\\z=1\cdot6-5=1\end{cases}}\)